Интеграл Лебега

Интеграл Лебега для простой функции. Функция 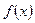, заданная на измеримом множестве Е наз. простой, если существуют такое мн-во 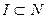, такие измеримые подмножества 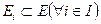и такие действительные числа 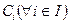, что выполнены след. соотношения: 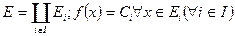(1). Простая функция 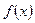зад. на измеримом мн-ве Е соотношением (1) наз. интегрируемой по Лебегу на Е (или суммируемой на Е), если сходиться числовой ряд: 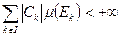. При этом интеграл Лебега от 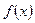на мн-ве Е наз. такое обозначаемое символом: 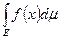действ. число, которое определяется след. равенством: 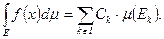(2). Из этого определения следует, что если только мн-во I входит в ф-лы (1) конечно, то заданная этой формулой фенкция 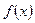заведомо интегрируема по Лебегу на Е.

Интеграл Лебега для измеримой функции. Функция 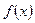, зад. на мн-ве Е наз. измеримой, если для 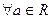мн-во 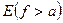явл. измеримым. (т.е. 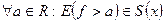). Измеримая функция 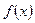, зад. на измеримом мн-ве Е, наз. интегрируемой по Лебегу на мн-ве Е (или суммируемой на Е), если существует последовательность 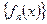простых, зад. на Е и интегрируемых по Лебегу на Е к функции 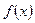.При этом интегралом Лебега от 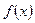по мн-ву Е наз. такое обозначаемое символом 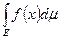действ. число, кот. определяется след. образом: 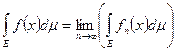(3).

Установим корректность заданного определения. Покажем, что предел, стоящий в правой части рав-ва (3) существует и конечен: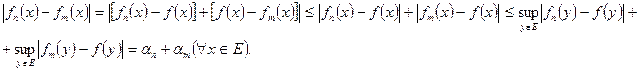

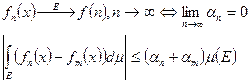(св-во 4 инт-ла Лебега)

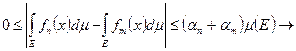(КритерийКоши) ;

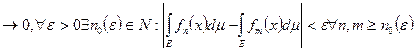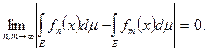
Т.о. существование конечного предела док-но в силу критерия Коши.

СВОЙСТВА ИНТЕГРАЛА ЛЕБЕГА.

Свойства инт. Лебега для простых функций. 1. Если Е- измеримое мн-во и 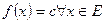, то такая функция 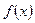интегрируема по Лебегу на Е и 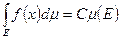. 2. Если простая функция 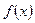зад. на измеримом мн-ве явл. интегрируемой по Лебегу на Е, то 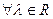функция 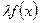также интегр. по Лебегу на Е 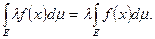3. Если простые функции 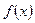, , 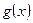зад. на измеримом мн-ве Е явл. суммируемы на Е, то и функция 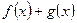также явл. суммируемой на Е и справедливо рав-во: 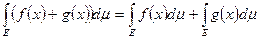(1). 4. Пусть простая функция 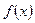, зад. на измеримом мн-ве Е явл. интегрируемой по Лебегу на Е и удовлетворяет условию: 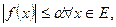(где 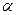-некоторое полож. число), тогда справедливо нер-во: .

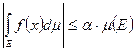Докажем св-во 3. Рассмотрим простой частный случай.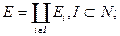

. .

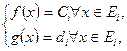
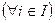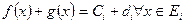
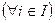В этом случае интегрир. 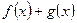, а также справедливость формулы (1) легко установить: ,

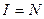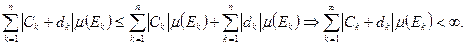
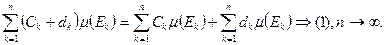
Свойства инт. Лебега выраженного нер-ми. 1. Пусть измеримая на Е функция 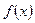удовл. условию: 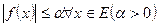. Тогда функция 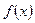интегр. по Лебегу на Е и справ-во нер-во: 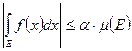. 2. Пусть измеримая на Е функция 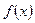удовл. нер-ву: 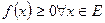. Тогда, если 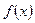интегрир. по Лебегу на Е,то 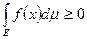. 3. Пусть измеримые на Е функци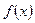и и 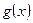итегрир. по Лебегу на Е и удовл. нер-ву: 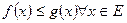. Тогда 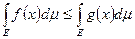. 4. Пусть измеримые на Е функци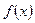и и 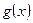удовл. нер-ву: 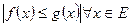. Тогда, если 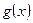интегрир. по Лебегу на Е, то и функция 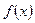также интегрир. по Лебегу на Е.