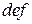2015-04-20
2767
Множество 
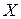называется метрическим пространством, если 
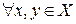определено неотрицательное число 
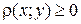, называемое расстоянием между элементам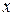и 
и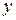 
и удовлетворяющее 3 аксиомам:
1. аксиома выбора: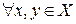 
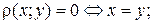
2. аксиома симметрии: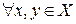 
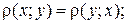
3. аксиома треугольника: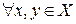 
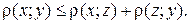
Если на множестве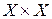 
задана функция 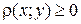удовлетворяющая 3 аксиомам из 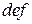, то эта функция называется метрикой заданной на .
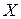Если на множестве 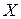задана метрика 
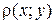, то полученное таким образом метрическое пространство принято обозначать 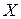или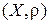 
, в зависимости от того нужно ли указывать каким образом задана метрика.
Элементы метрического пространства принято называть точками этого пространства.
Примеры метрических пространств:
1. На множестве всех упорядоченных совокупностей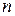 
действительных чисел зададим 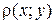следующим образом
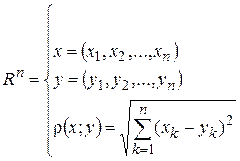
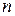- мерное Евклидово пространство
2. На множестве всех ограниченных числовых последовательностей зададим 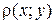следующим образом
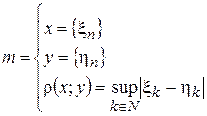- пространство ограниченных числовых последовательностей
3. Пусть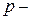 
фиксированное число 
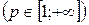, на множестве всех числовых последовательностей 
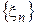, каждая из которых удовлетворяет условию сходимости числового ряда 
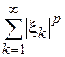, зададим 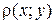следующим образом
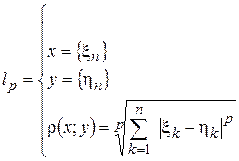- пространство числовых последовательностей суммируемых со степенью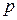 
4. На множестве всех числовых последовательностей зададим 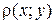следующим образом
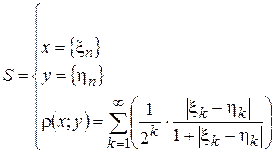- пространство числовых последовательностей
5. На множестве всех действительных функций определенных и непрерывных на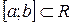 
зададим 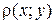следующим образом
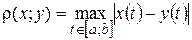. Полученное таким образом пространство обозначается символом 
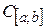и называется пространством функций непрерывных на 
.
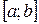6. На множестве всех определенных на 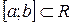и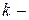 
раз непрерывно дифференцируемых функций зададим 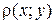следующим образом
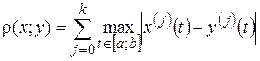, где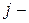 
производная. Полученное таким образом пространство обозначается символом 
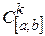и называется пространством 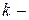раз непрерывно дифференцируемых на 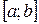функций.
7. На множестве всех определенных и ограниченных на 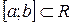функций зададим 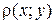следующим образом
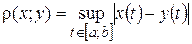. Полученное таким образом пространство обозначается символом 
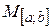и называется пространством ограниченных на 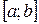функций.
8. Пусть 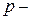фиксированное число 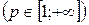, на множестве всех вещественных функций 
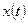каждая из которых удовлетворяет 3 условиям:
1) 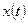- определена на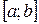
2) 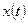- измерима по Лебегу на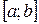
3) 
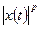- интегрируема по Лебегу на .
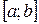Зададим 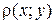следующим образом: 
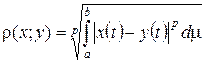. Полученное таким образом пространство обозначается символом 
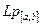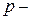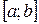и называется пространством суммируемых со степенью на функций.
Сходимость последовательностей элементов метрических пространств.
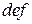Будем говорить, что последовательность элементов 
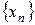метрического пространства 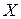, является сходящейся (сх) в этом пространстве к элементу 
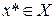, если: 
.
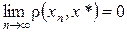Св-ва:
1)всякая сходящаяся последовательность элементов метрического пространства сходится к единственному элементу этого пространства;
2)каждая сходящаяся последовательность метрического пространства является ограниченной;
3)любая подпоследовательность сходящейся последовательности элементов метрического пространства сходится к тому же элементу этого пространства, что и сама последовательность;
4) всякая сходящаяся последовательность элементов метрического пространства сходится в себе;
5) всякая сходящаяся в себе последовательность элементов метрического пространства является ограниченной.
