Опр. Линейное (векторное) пространство над полем наз множ (Эл которого наз векторами) на котором введено 2 операции сложения и умножения на число (элем поля) и выполн. след. аксиомы:
0) 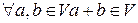
1) 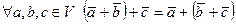
2) 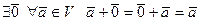
3) 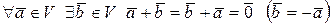
4) 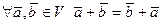
5) 
6) 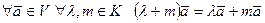
7) 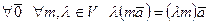
8) 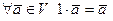 .
.
В качестве поля мы будем рассматривать в поле как в множ. действит чисел (в этом случае пространство наз. действит.) и поле (множ. комплексных чисел), если не оговорено противоположное рассматривается действительное пространство.
Опр. Вектор – это элемент векторного пространства.
Опр. Базисом ЛВП – наз. любая упорядоченная макс лин. независимая система векторов (любые 2 базиса пространства имеют одинаковое количество векторов.)
Опр. Размерностью лин. пространства наз. число = кол-ву элементов в любом базисе этого пространства (в лин пространстве не определено понятие длинны вектора и угла между векторами).
Опр. Координатами вектора 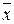 в базисе наз. упорядоченный набор коэффициентов
в базисе наз. упорядоченный набор коэффициентов 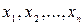 при разложении данного вектора по базису. (Пример:
при разложении данного вектора по базису. (Пример: 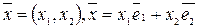 или
или 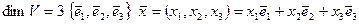 )
)
Опр. Подпространством лин векторного пространства наз такое его подмножество, которое само явл лин простр-м относительно тех же операций.
Критерий под-ва. Подпространство 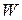 лин. векторного пр-ва
лин. векторного пр-ва 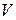 явл. подпр-вом
явл. подпр-вом 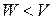 тогда и только тогда, когда выполняются две аксиомы:
тогда и только тогда, когда выполняются две аксиомы:
1) 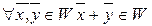 (сумма 2-х елементов из подмнож лежит в этом подмнож.)
(сумма 2-х елементов из подмнож лежит в этом подмнож.)
2) 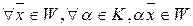 (Произведение любого числа на любой элемент подмнож лежит в этом подмнож)
(Произведение любого числа на любой элемент подмнож лежит в этом подмнож)
Базис подпространства всегда можно дополнить до базиса всего пространства.
Опр. Пересечением (объединением) подпространств 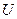 и
и 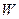 наз множ тех векторов кот входят в
наз множ тех векторов кот входят в 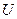 и
и 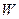 одновременно (кот входят или в
одновременно (кот входят или в 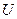 или в
или в 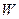 )
)
Опр. Суммой подпространств 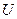 и
и 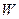 наз множ векторов каждый из кот можно записать в виде суммы 2-х векторов одного из
наз множ векторов каждый из кот можно записать в виде суммы 2-х векторов одного из 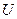 другого из
другого из 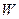
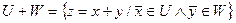
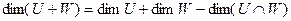 - формула Грассмана.
- формула Грассмана.
Опр. Сумма подпространств наз прямой 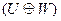 если пересечение этих подпространств состоит только из
если пересечение этих подпространств состоит только из 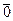 .
.
 2015-04-20
2015-04-20 623
623








