Полная и средняя кривизна поверхности. Понятие внутренней геометрии поверхности

Полной или Гауссовой кривизной поверхности в точке М называется произведение главных кривизн поверхности в этой точке, а средней кривизной – полусумма главных кривизн: K=k₁k₂ H= .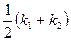

Теорема (о вычислении главных кривизн): Полная кривизна поверхности в точке 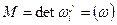, средняя кривизна 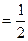следа этой матрицы. Доказательство: 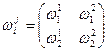. Перейдем к базису, составленного из соответственных векторов. Тогда 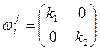, тогда , .

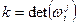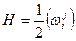Теорема: Главные кривизны к₁ и к₂ поверхности в точке М являются решением уравнения: 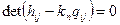для полной кривизны: . .

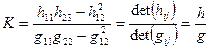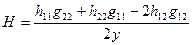Теорема: Координаты du и dv главного направления поверхности находяться из уравнения: 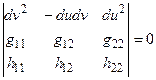. (1) Доказательство: Главное направление – это собственный векторный оператор. Пусть 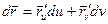- вектор главного направления из уравнения 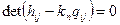. Тогда, координаты du и dv является решением однородной системы уравнений: 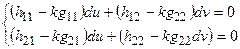=> 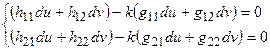. Найдем и подставим: => .

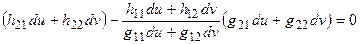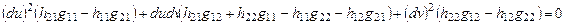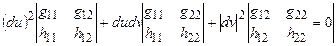(2). Уравнения (1) и (2) – эквивалентны. Теорема доказана.