Определителем (детерминант) 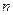 -го порядка наз сумма
-го порядка наз сумма 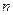 ! слагаемых каждый из которых есть произв
! слагаемых каждый из которых есть произв 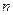 - елементов взятых по одному из каждой строки и каждого столбца с учетом правила знака.
- елементов взятых по одному из каждой строки и каждого столбца с учетом правила знака.
Правило знака: слагаемые входит в определитель со знаком + (-), если подстановка 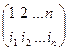 является четным (нечетным)
является четным (нечетным)
Св-ва опред-й. 1) определитель транспонированной мат = опред исходной матр 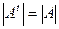 .
.
2) общий множитель в строке можно выносить за знак опред.
3) если какая-то строка определителя представляет собой сумму 2-х строк, то этот опред = сумме 2-х опред в каждом из кот вместо этой строки состоит соответствующая строка слагаемых.
4) опред содержащий нулевую строку =0.
5) если в опред. поменять местами 2 строки то он изменит знак
6) определ с 2-мя равными строками =0
7) опред с 2-мя пропорциональными строками =0 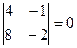
8)опред не изменится если к какой-нибудь его строке прибавить другую строку умноженную на некоторое число.
9) опред верхнетриугольной матр = произведению диагональных елементов.
10) разложение опред по строке – опред = сумме произведений элементов некоторой строки на алгебр дополнение к элементам этой строки. (Дополнительным минором 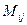 к элем-ту
к элем-ту 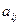 наз опред. получ. вычеркиванием из исходного опред.
наз опред. получ. вычеркиванием из исходного опред. 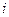 строки и
строки и 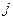 столбца. Алгебраич дополнением
столбца. Алгебраич дополнением 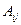 к эл-ту
к эл-ту 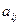 наз исходный опред. в котором
наз исходный опред. в котором 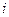 строке и
строке и 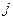 столбце стоят 0, а на их пересечениях единицы (Минором Мij Эл-та aij опред-я n-го пор-ка наз-ся опрде-ль n-1 порядка, который получается из опред-я вычеркиванием i строки и j столбца. Алгебаическим дополнением Aij Эл-та aij наз-ся произ-е (-1)i+j*Mij.))
столбце стоят 0, а на их пересечениях единицы (Минором Мij Эл-та aij опред-я n-го пор-ка наз-ся опрде-ль n-1 порядка, который получается из опред-я вычеркиванием i строки и j столбца. Алгебаическим дополнением Aij Эл-та aij наз-ся произ-е (-1)i+j*Mij.))
11) сумма произведений элементов некоторой строки опреднлителя на алг. дополнение к элементам другой строки равна 0.
12) сумма произвед элем строки 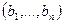 на алгебр дополн. к элем.
на алгебр дополн. к элем. 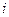 строки опред
строки опред 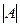 = опред
= опред 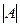 в котором вместо
в котором вместо 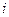 строки стоит строка
строки стоит строка 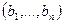 .
.
13) Теорема Лапласса: Выберем в определители n-го порядка m-строк, тогда исходный определитель будет равен сумме произведения всевозможных миноров сост-их из выбранных строк на их алг. дополнение.
14) опред произведения квадратн матр = произвед опред 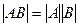
 2015-04-20
2015-04-20 506
506








