Опр. Линейное (векторное) пространство над полем наз множ (Эл которого наз векторами) на котором введено 2 операции сложения и умножения на число (элем поля) и выполн. след. аксиомы:
0) 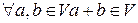
1) 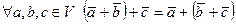
2) 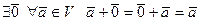
3) 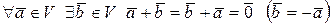
4) 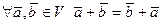
5) 
6) 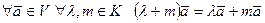
7) 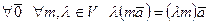
8) 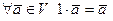
Опр. Пусть 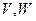 - 2 лин пространства. Отображение
- 2 лин пространства. Отображение 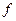 из
из 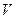 в
в 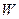 наз линейным если выполн. аксиомы: 1)
наз линейным если выполн. аксиомы: 1) 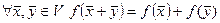 2)
2) 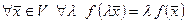 .
.
Опр. Лин оператором наз лин отображение векторного пространства в себя..
Опр. Матрица лин оператора в данном базисе наз матр  по столбцам кот записаны корд образов базисных векторов в этом базисе.
по столбцам кот записаны корд образов базисных векторов в этом базисе.
Опр. Ядро лин оператора наз. множ всех векторов лин пр-ва 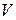 , кот этот оператор переходят в нулевой вектор.
, кот этот оператор переходят в нулевой вектор. 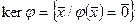
Опр. Дефектом лин опер наз размерность его ядра (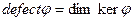 ).
).
Опр. Образом оператора 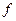 наз. мн-во Im
наз. мн-во Im 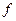 всех векторов пр-ва
всех векторов пр-ва 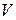 , каждый из кот-х имеет прообраз (то есть
, каждый из кот-х имеет прообраз (то есть 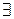 такие вектора в которые лин оператор
такие вектора в которые лин оператор 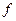 переводит вектора из лин векторного пр-ва
переводит вектора из лин векторного пр-ва 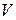 )
)
Опр. Ранг лин опер наз размерность его образа 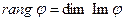 .
.
Th: Для любого лин опер 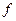 вектор-го пр-ва
вектор-го пр-ва 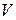 имеет место следующее равенство
имеет место следующее равенство 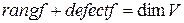
 2015-04-20
2015-04-20 541
541








