2015-04-20
503
Линейное (векторное) пространство над полем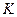 
называется множество (Элементы которого называются векторами) на котором введено 2 операции сложения и умножения на число (элементы поля 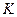) и выполняются следующие аксиомы: 1)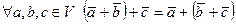 
2) 
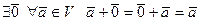
3) 
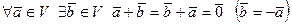
4) 
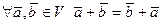
5) 
6) 
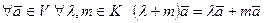
7) 
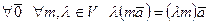
8) 
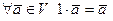
Пусть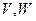 
- 2 линейных пространства. Отображение 
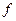из 
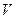в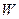 
называется линейным если выполняются аксиомы:
1) 
,
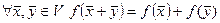2) 
.
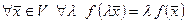Линейным оператором называется линейное отображение векторного пространства в себя.
Вектор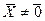 
(ненулевой 
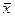) называется собственным вектором линейного оператора 
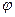если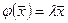 
при этом число 
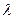называется собственным значением оператора .
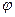Число 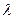называется собственным числом линейного оператора 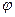если существует такой ненулевой 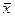что .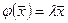
Теорема: собственные векторы отвечающие различным собственным значениям линейно не зависимы.
Следствие: кол-во собственных значений линейного оператора превосходит размерности пр-ва.
Множество всех собственных значений линейного оператора называется спектром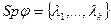 
.
Если 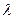собственное значение оператора 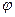то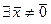 
. Система уравнений 
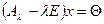кот должна иметь нетривиальное решение, то есть нулевое.
Используя теорему Крамера получаем, что данная система будет иметь не тривиальное решение тогда и только тогда, когда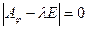 
полученное уравнение называется характеристическим, собственные значения и только они являются корнями характеристического уравнения.
Теорема: Для того, чтобы комплексное число l было собственным значением линейного оператора А необходимо и достаточно, чтобы это число являлось корнем характеристического уравнения det (А-lI)=0.
