Квадратичні форми. Ма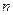триця квадратичної форми. Зведення квадратичної форми до канонічного виду

Квадратичной формой переменных наз однородный многочлен второй степени зависящий от 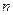переменных.

Многочлен 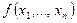называется однородным в степени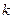

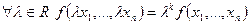
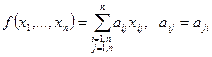общий вид квадратич формы. Говорят что квадратичная Форма имеет канонический вид если ее матрица является диагональной если все коэфициенты стоящие не при квадратных переменных =0. Квадратичная форма имеет нормальный вид если ее матрица является диагональной и все элементы главной диагонали = или 1, или -1, или 0, или коэфиц при квадрат форме =1, -1, 0, а все остальные коэфиц =0

Преобразование переменных называется линейным если оно имеет вид 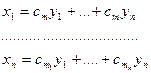или в матричной форме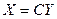

Линейное преобразование называется невырожденным если матр 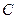- невырожденная

Приведение к каноническому виду: Путем невырожденного линейного преобразования(НЛП) вид квадратичной формы можно упростить к тому чтобы она имела канонический вид.

Наиболее простым способом приведения квадратичной формы является Метод выделения полного квадрата (Метод Лагранжа).

Пусть дана квадрат форма 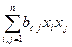1)

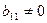если , то 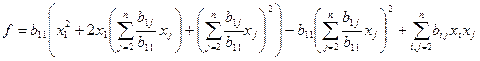сделаем замену переменных:

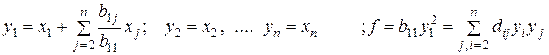
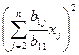- это слагаемое есть квадратичная форма меньшая числа и к ним применяем то же самое

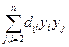- коэффициент при квадратичной переменной =0 и существует хотя бы один коэфициент при квадрате 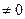то поменяем местами переменные и сведем задачу к предыдущей.

Опр. Две квадратичные формы называются эквивалентными если 1) они зависят от одинакового количества переменных 2) сущ НЛП переводящее одну из них в другую.

Th: 2 квадрат формы от одинакового числа переменных эквивалентны т и т т когда у них совпадают ранги и сигнатуры.

Опр. Две квадратичные формы над полем 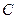наз эквивалентными если они содержат одинаковое число неизв и сущ НЛП переводящее одну в другую.

Th: Две квадратичные формы над полем 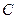зависящие от одинак числа перемен эквивалентны т и т т когда у них совпад ранги.

Опр. Квадратичная матрица называется унитриугольной если она является верхнетреугольной и по главной диагонали стоят еденицы.

Th: пусть ранг квадратичной формы = 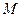если первые 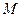угольных миноров матрицы квадратичной формы отличны от нуля то существует унитриугольное преобразование приводящее квадратичную форму к каноническому виду. 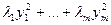, , 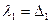, 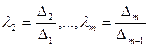здесь 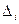- это 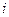-й главный угловой минор.