Сопряженные операторы. Самосопряженные операторы

def

Пусть Е - евклидово пространство и 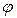- оператор, действующий в этом евклидовом пространстве. Тогда сопряженным оператором к 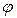наз. такой оператор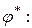

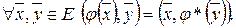
Th

Для любого оператора в евклидовом пространстве существует единственный сопряженный оператор.

Замечание!

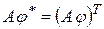- в ортонормированном базисе;

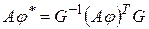- в произвольном базисе,

где 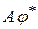- матрица сопряженного оператора.

Свойства операции сопряжения

1)

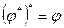
2)

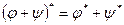
3)

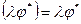
4)

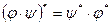
def

Оператор 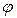действующий в евклидовом пространстве V наз. самосопряженным, если он совпадает со своим сопряженным оператором, т.е. 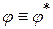или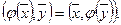

Замечание!

В ортонормированном базисе матрица самосопряженного оператора является симметрической.

Th(О собственных значениях самосопряженного оператора)

Все собственные значения самосопряженного оператора являются действительными.