2015-04-20
629
Квадратичной формой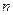 
переменных называется однородный многочлен второй степени зависящий от 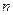переменных.
Многочлен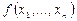 
называется однородным в степени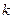 
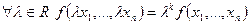
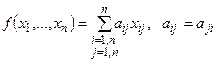общий вид квадратичной формы.
Говорят что квадратичная Форма имеет канонический вид если ее матр явл диагональной если все коэфициенты стоящие не при квадратных переменных =0
Квадратичная форма имеет нормальный вид если ее матрица является диагональной и все элементы главной диагонали = или 1, или -1, или 0, или коэфициенты при квадратичной форме =1, -1, 0, а все остальные коэфициеннты =0.
Квадратичная Форма наз положит е льно определенной (отрицательно определенной) если при любых значениях переменных (кроме случая когда они все =0 одновременно) квадратичная Форма принимает положительные (отрицательные) значения. (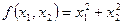
- положительно определенная; 
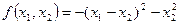- отрицательно определенная). Квадратичная Форма положительно определенная если 1) 
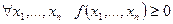, 2)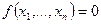 
т и т т когда 
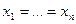. Квадратичная Форма называется неотрицательно определенной (полуопределенной) если она может принимать только неотрицательные значения (
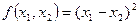- неотрицательная. 
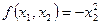- неположительная.).
|
|
|
На практике используют критерий Сильвестра: квадратичная Форма будет положительно определенной т и т т когда все главные миноры >0.
Приведение к ф к каноническому виду при помощи ортогональных преобразований
1) записываем матрицу квадратичной формы и строим характеристический многочлен
2) находим собственные значения
3) записываем канонический вид квадратичной формы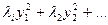 
где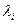 
- это собственные значения
4) находим собственные вектора
5) если все собственные значения различные то нормируем (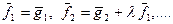
где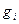 
- собственный вектор)
Если есть кратные собственные значения то полученные собств векторы отвечающие этим собственным значениям предварительно ортогонализируют
6) записываем мат перехода и запис соотв преобразования.
Приведение пары квадратичных Форм к канонич виду при помощи одного НЛП( невырожденного линейного преобразования ):
1) находим какая из форм является положительно определенной (Критерий Сильвестра)
2) Методом Лагранжа положительно определенную квадратичную форму приводим к нормальному виду. Находим как меняется при этом 2-я
3) С помощью ортогонального преобразования измененную 2ю квадратичную форму приводим к каноническому виду при этом 1-я форма остается в нормальном виде
4) Выписываем требуемое преобразование как композицию 2-х преобразований
Метод выделения полного квадрата (Метод Лагранжа).
Пусть дана квадратичная форма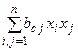 
1) если 
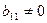, то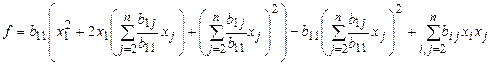 
сделаем замену переменных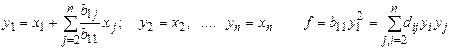 
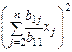- это слагаемое есть квадратичная форма меньшая числа и к ним применяем то же самое
|
|
|
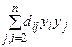- коэффиц при квадр переем =0 и существует хотя бы один коэфициент при квадрате 
то поменяем местами переменные и сведем задачу к предыдущей.
