Высказывание –это повествовательное предложение о котором можно сказать, что оно истинно или ложно (2*3=5 –ложное). Высказывания могут являться истинными или ложными.
Логические операции над высказываниями:
1. Отрицание 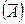 – высказывание А, высказывание не А которое истинно тогда
– высказывание А, высказывание не А которое истинно тогда
и только тогда, когда А – ложное.
2. Коньюнкция (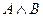 )– высказывание А и В, которое истинно тогда и только
)– высказывание А и В, которое истинно тогда и только
тогда, когда А – истинно и В – истинно.
3. Дезьюнкция (АvВ (А или В)) – высказывание А и В которое ложно, если А
и В – ложны.
4. Импликация (А => B) – высказывание А и В, которое будет ложно т. и т. т.,
к. А –истино и В – ложно.
5. Эквиваленция (АóB)– высказывание А и В, которое истино т. и т. т., к. А=В.
Теперь построим таблицу истинности для данных высказываний:
| А | В | 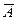 | 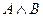 | АvВ | А => B | АóB |
Формула логики высказываний называется тавтологией, если она истина при
любых значениях, входящих в нее элементарных высказываний. Например:
| А | 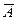 | Аv 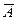 |
Формула логики высказываний называется тождественно ложной (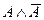 ), если она ложна при любых значениях, входящих в нее элементарных высказываний. Формула В (А1,…,Аn
), если она ложна при любых значениях, входящих в нее элементарных высказываний. Формула В (А1,…,Аn 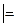 В) называется логически выводимой из А1,…,Аn, если при любом выборе элементарных высказываний, входящих в состав формулы А1,…,Аn формула В будет истина всякий раз, когда будет истина вся формула А1,…,Аn. Формулы А и В называются равносильными и ли логически эквивалентными, если они принимают одинаковые значения при любом выборе элементарных высказываний (т.е. если их таблицы истинности совпадают).
В) называется логически выводимой из А1,…,Аn, если при любом выборе элементарных высказываний, входящих в состав формулы А1,…,Аn формула В будет истина всякий раз, когда будет истина вся формула А1,…,Аn. Формулы А и В называются равносильными и ли логически эквивалентными, если они принимают одинаковые значения при любом выборе элементарных высказываний (т.е. если их таблицы истинности совпадают).
Законы Де – Моргана: 1) 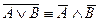 ; 2)
; 2) 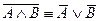 .
.
Теорема: 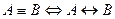 - тавтология.
- тавтология.
Можно привести такие наиболее встречающиеся формулы логических высказываний:
1) 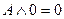
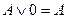 5)
5) 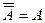 9) (А*В)*С=А*(В*С
9) (А*В)*С=А*(В*С
2) 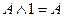
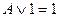 6)
6) 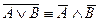 10) (АvВ)
10) (АvВ) 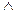 С=АСvВС
С=АСvВС
3) 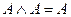
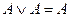 7)
7) 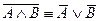 11)
11) 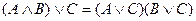
4) 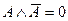
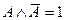 8) А*В=В*А 12) АvАВ=А
8) А*В=В*А 12) АvАВ=А
13) А=>В= 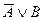
14) АóВ=(А=>B)(B=>A) 17) AóB= 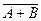
15) AóB= 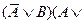
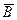 ) 18) A
) 18) A 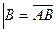
16) AóB=AB 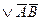 19)
19) 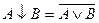
 2015-04-20
2015-04-20 2974
2974
