Два целых числа а и в сравнимы по модулю натурального числа m є N, если при делении на m они дают одинаковый остаток. 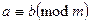 .
.
Теорема (критерий сравнимости): 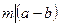 . Следствие 1: каждое число сравнимо по модулю m со своим остатком от деления на m:
. Следствие 1: каждое число сравнимо по модулю m со своим остатком от деления на m: 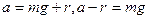 . Следствие 2: число сравнимо по модулю m, т. и т. т., к. оно делится на этот mod.
. Следствие 2: число сравнимо по модулю m, т. и т. т., к. оно делится на этот mod.
Основные свойства сравнения: 1). Относительные сравнения являются относительно эквивалентными. 2). Сравнения по одному и тому же модулю можно почленно вычитать: 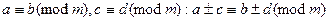 . Слагаемое можно переносить из одной части в другую, при этом знак меняем на противоположный. 3). В каждой части сравнения можно прибавлять любое число, кратное модулю:
. Слагаемое можно переносить из одной части в другую, при этом знак меняем на противоположный. 3). В каждой части сравнения можно прибавлять любое число, кратное модулю: 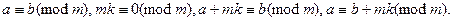 сравнения по одному и тому же модулю можно почленно умножать. Следствия: 1. Обе части сравнения можно возводить в любую натуральную степень. 2. Обе части сравнения можно умножать на любое натуральное число. 4). Обе части сравнения и модуль можно умножить на одно и то же число или сократить на любой их общий делитель. 5). Если сравнение имеет место по нескольким модулям то оно имеет место и по модулю, который равен их наибольшему кратному или наибольшему общему делителю
сравнения по одному и тому же модулю можно почленно умножать. Следствия: 1. Обе части сравнения можно возводить в любую натуральную степень. 2. Обе части сравнения можно умножать на любое натуральное число. 4). Обе части сравнения и модуль можно умножить на одно и то же число или сократить на любой их общий делитель. 5). Если сравнение имеет место по нескольким модулям то оно имеет место и по модулю, который равен их наибольшему кратному или наибольшему общему делителю 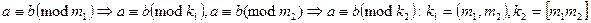
6). Если сравнение имеет место по модулю m, то оно имеет место и по любому
делителю числа m. 7). Общий делитель одной части сравнения и модуль является делителем другой части сравнения: 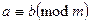 ,
, 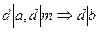 .
.
Малая теорема Ферма: если a и m – взаимнопростые числа, тогда 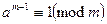 . Функция Эйлера – это число положительных чисел, не превосходящие n и взаимнопростые с n. Если целое число a взаимнопростое с m, то
. Функция Эйлера – это число положительных чисел, не превосходящие n и взаимнопростые с n. Если целое число a взаимнопростое с m, то 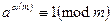 . Теорема Эйлера: если целое число a взаимнопростое с m, то
. Теорема Эйлера: если целое число a взаимнопростое с m, то 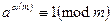 . Теорема Ферма: 1. Если целое число a не делит p, где р – простое, то
. Теорема Ферма: 1. Если целое число a не делит p, где р – простое, то 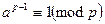 . 2. Если р – простое и а –любое целое число, тогда
. 2. Если р – простое и а –любое целое число, тогда 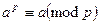 . Отношение сравнимости – это классы эквивалентности. Классы эквивалентности также называются классами вычетов, а их эквивалентности называют вычетами.
. Отношение сравнимости – это классы эквивалентности. Классы эквивалентности также называются классами вычетов, а их эквивалентности называют вычетами.
Решение сравнений: Пусть 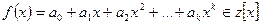 ,
, 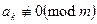 , mєN. Тогда
, mєN. Тогда  называется сравнением к – степени с одним неизвестным и имеет не более, чем m классов решений. Решениями данного сравнения будут являться классы вычетов по модулю m. Сравнения первой степени с одной неизвестной можно записать в виде:
называется сравнением к – степени с одним неизвестным и имеет не более, чем m классов решений. Решениями данного сравнения будут являться классы вычетов по модулю m. Сравнения первой степени с одной неизвестной можно записать в виде: 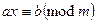 если: 1).
если: 1). 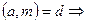 это сравнение не имеет решения (например 5x
это сравнение не имеет решения (например 5x 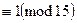 ). 2). Если
). 2). Если 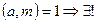 решение этого сравнения. 3).
решение этого сравнения. 3). 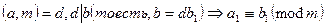 .
.
Теорема: Пусть 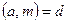 ,
, 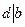 , то
, то 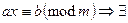 , d – класов решений mod m. Методы решения сравнений: 1). Метод испытания полной системы вычетов. 2). Метод преобразования коэффициентов. Прибавляется или вычитается из правой части любое число, кратное модулю, заменяя коэффициенты в левой части на число сравнений с модулем. Можно преобразовать сравнения так, что его можно будет сократить на а и получить решение.
, d – класов решений mod m. Методы решения сравнений: 1). Метод испытания полной системы вычетов. 2). Метод преобразования коэффициентов. Прибавляется или вычитается из правой части любое число, кратное модулю, заменяя коэффициенты в левой части на число сравнений с модулем. Можно преобразовать сравнения так, что его можно будет сократить на а и получить решение.
Пример: 5x 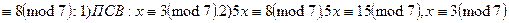 . 3). Решение сравнений с помощью системы Эйлера:
. 3). Решение сравнений с помощью системы Эйлера: 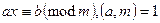 . Тогда
. Тогда 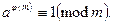
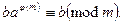
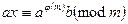 .
. 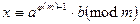 . (5х
. (5х 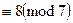
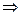
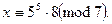 =>
=> 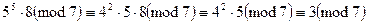 ).
).
 2015-04-20
2015-04-20 4275
4275
