Функция вида 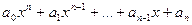 , в которой
, в которой 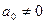 наз. многочленом степени
наз. многочленом степени 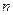 . Числа
. Числа 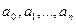 наз. коэфициентами многочлена (в общем случае они будут комплесными), а
наз. коэфициентами многочлена (в общем случае они будут комплесными), а 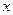 наз. переменной, которая принимает любые комплесные значения.
наз. переменной, которая принимает любые комплесные значения.
Два мн-на наз. равными, если совпадают их степени и совпадают коэф-ты при соответствующих степенях переменных.
1 Теорема Безу: остаток 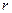 от деления мн-на
от деления мн-на 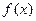 на мн-н
на мн-н 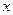 -с равен значению мн-на
-с равен значению мн-на 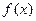 при
при 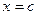 , т. е.
, т. е. 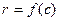 .
.
2 Теорема Безу: Число 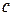 будет корнем многочлена
будет корнем многочлена 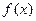 , тогда и только тогда, когда
, тогда и только тогда, когда 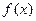 делится на
делится на 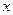 -с без остатка.
-с без остатка.
Теорема Штурма: если многочлен 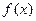 с действ. коэф-ми не имеет кратных корней, то кол-во корней на промежутке
с действ. коэф-ми не имеет кратных корней, то кол-во корней на промежутке 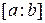 равно разности кол-ва переменных знаков в последовательности Штурма, вычисленных в точках
равно разности кол-ва переменных знаков в последовательности Штурма, вычисленных в точках 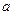 и
и 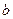 , т.е.
, т.е. 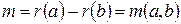 .
.
 2015-04-20
2015-04-20 768
768








