2015-04-20
599
Лин. неодн. ур-е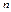 
-го порядка имеет вид
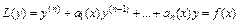(1)
где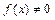 
, 
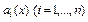- непр-ны на инт-ле 
.
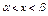Общее реш-е ур-я (1) нах-ся по ф-ле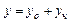 
(2)
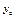- общее реш-е лин. одн. ур-я 
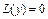, соответствующего ур-ю (1), а 
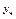- к-нибудь частное реш-е неодн. ур-я (1)
Опр. ФСР – любые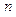 
лин. независимых реш-й ур-я 
.
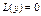1. Если сущ. ФСР, то общ. реш-е неодн. ур-я (1) м. б. найдено с пом Метода вариации произвольных постоянных (Лагранжа).Сущность этого метода сост. в след. Общее реш-е неодн. ур-я (1) ищем в виде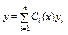 
(3)
где ф-и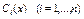 
опр-ся из сист. ур-й
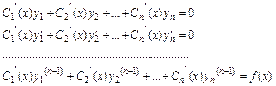(4Относ. 
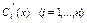(4) явл. сист. 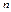лин. неодн. алгебраич. ур-й, причем главный определитель сист.
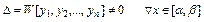(5)
Поэтому сист. (4) имеет единств. реш-е:
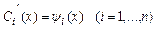, (6)
откуда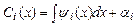 
(7)
где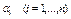 
- произвольные постоянные. Учитывая рав-ва (3) и (7), общее реш-е неодн. ур-я, найденное методом вариации произвольных постоянных, получаем в виде
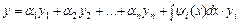(8)
2. Метод неопр коэф-тов.
Пусть 
, где 
, 
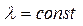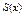- многочлен степени 
.
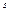1)Если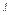 
не совпадает ни с одним корнем х-кого ур-я. Тогда
,
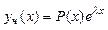где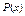 
- многочлен той же степени, что и .
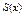2)Если 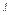совпадает с корнем х-кого ур-я кратности 
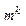. Тогда
,
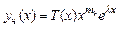где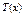 
- многочлен той же степени, что и .
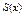Пусть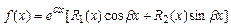 
1) 
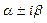- не явл. корнем х-кого ур-я
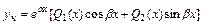
где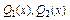 
- многочлен той же степени, что и 
.
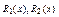2) 
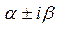- явл. корнем х-кого ур-я
