Решение систем дифференциальных уравнений методом исключений

Одним из основных методов интегрирования системы дифференциальных уравнений является сведение к уравнению более высокого порядка, состоящего в следующем: из уравнений системы 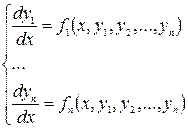(1)

и из уравнений, получающихся дифференцированием уравнения, входящего в систему, исключают все неизвестные функции, кроме одной, для определения которой получают одно дифференциальное уравнение более высокого порядка. Интегрируя, находят одну из неизвестных функций, а остальные функции определяют из исходных уравнений и уравнений, получившихся в результате их дифференцирования.

Дифференцируя по х первое из уравнений системы (1):

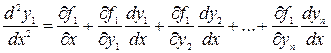
Заменяя производные 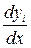, 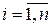на 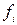, 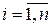из системы (1) получим:

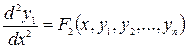
Дифференцируя полученное уравнение и поступая аналогично предыдущего, получим:

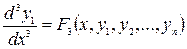
Продолжая указанную процедуру, получим последнее уравнение:

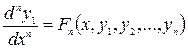
Итак, получим систему

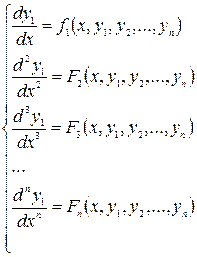(2)

Из первых (n -1) уравнений определим 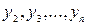, выразив их через 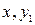и производные , , ,…,

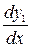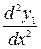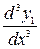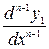
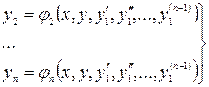(3)

Подставляя выражения (3) в последнее из уравнений системы (2), получим уравнение n -го порядка для определения .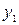

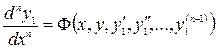
Решая это уравнение, определим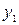

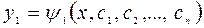(4)

Дифференцируя (4) (n -1) раз найдём производные 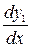, ,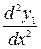…, 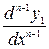как функции от .

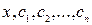Подставляя их в выражение (3), получим

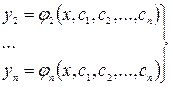(5)

Тогда выражения (4) и (5) дают решение системы (1). Если дана задача Коши, то из уравнений (4) и (5) определяют значения произвольных констант , .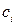

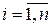Замечание 1

указанный процесс исключения всех функций, кроме одной предполагает, что определитель

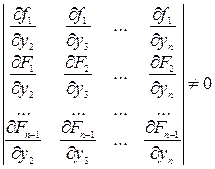
Только в этом случае, система (2) будет разрешима относительно функций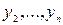

Замечание 2

Если применить выше указанный метод к линейной однородной системе 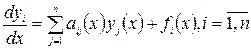, то уравнение n -го порядка будет линейным однородным. При чём если все коэффициенты 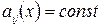, то и уравнение будет линейным однородным уравнением с постоянными коэффициентами. Аналогичное замечание справедливо и для линейной неоднородной системы, для которой уравнение будет линейным неоднородным уравнением n -го порядка.