Решение нелин. алгебраических ур-ий методом Ньютона

Этот метод весьма эффективен для решения алгебраич. Ур-й. Его основное преимущество состоит в том, что при сравнительно простой схеме вычислений он обладает быстрой сходимостью.

Пусть единственный корень 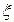ур-ия

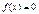(1)

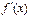расположен внутри интервала , причем и 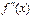непрерывны и сохраняют определенные знаки . .

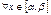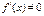Пусть нач. прибл-е 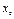известно. Заменим 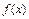отрезком из ряда Тейлора

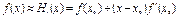и за следующее прибл-е 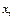возьмем корень уравнения 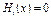, т. е.

.

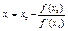Вообще, если итерация 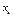известна, то следующее приближение 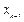в методе Ньютона определяется по правилу

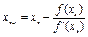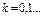, (2)

Нач. прибл-е 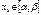и должно удовлетворять условию

(3)

Метод Ньютона наз-ют также методом касательных, так как новое прибл-е 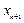является абсциссой точки пересечения касательной, проведенной в точке 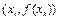к графику функции 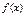, с осью .

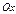Этот метод имеет квадратичную сходимость, т. е. в отличие от линейных задач погрешность на следующей итерации пропорциональна квадрату погрешности на предыдущей итерации: .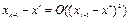

Для оценки точности приближения 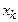можно воспользоваться формулой

,

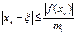где ,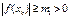

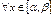
Метод Ньютона обладает очень быстрой сходимостью. Такая быстрая сходимость гарантируется лишь при очень хороших, т. е. близких к точному решению нач. прибл-ях. Если нач. прибл-е выбрано неудачно, то метод может сходиться медленно, либо не сойдется вообще.