Пусть функция y = f (x) определена, строго монотонна и непрерывна в некоторой окрестности точки x 0, дифференцируема в точке x 0, причём производная f '(x 0) ¹ 0. Тогда в некоторой окрестности точки у 0(где у 0 = f (x 0)) существует обратная функция x = f -1(y), эта обратная функция дифференцируема в точке у 0, и f -1'(y 0)= 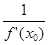 .
.
Доказательство:
(рисунок)
Из условий теоремы следует: $ [ a, b ]: y = f (x) определена, строго монотонна и непрерывна на [ a, b ]. причём a < x 0 < b. Поэтому, согласно теореме 3.5, множеством значений f (x), рассматриваемой на [ a, b ], является сегмент Y = [ f (a), f (b)], на Y существует обратная функция x = f -1(y), строго монотонная и непрерывная. При этом y 0 Î (f (a), f (b)). Зададим приращение D y ¹ 0 аргументу обратной функции в точке y 0. Обратная функция получит приращение D х = f -1(y 0 + D y) - f -1(y 0), причем D х ¹ 0 в силу строгой монотонности обратной функции. Рассмотрим равенство:
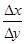 =
= 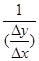 . (1)
. (1)
Пусть D y ® 0, тогда D х ® 0 в силу непрерывности обратной функции. Но при D х ® 0 знаменатель в правой части равенства (1) стремится к f '(x 0), причем по условию f '(x 0) ¹ 0. Поэтому при D y ® 0 предел правой части равен 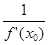 . Следовательно при D y ® 0 существует предел левой части равенства (1), то есть существует производная обратной функции в точке у 0 и она равна
. Следовательно при D y ® 0 существует предел левой части равенства (1), то есть существует производная обратной функции в точке у 0 и она равна 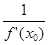 : f -1'(y 0)=
: f -1'(y 0)= 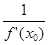 .
.
 2015-04-20
2015-04-20 667
667








