Достаточное условие непрерывности функции в точке

Пусть f (x) определена на [ a, a + d). Функция f (x) называется непрерывной в точке а справа, если 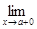f (x) = f (а). (то есть f (а + 0) = f (а)).

Аналогично определяется непрерывность в точке а слева.

Пример:

f (x) = [ x ].

(рисунок)

" целого n: f (n - 0) = n - 1, f (n + 0) = n, f (n) = n, то есть, f (n + 0) = f (n) ¹ f (n - 0).

Следовательно, в целочисленных точках эта функция непрерывна только справа. В остальных точках- и справа и слева.

Теорема 3.1

Если f (x) непрерывна в точке а справа и слева, то она непрерывна в точке а.

Доказательство:

По условию f (а + 0) = f (а) и f (а - 0) = f (а).

Отсюда по теореме 2.1 (Если в точке a правое и левое предельные значения функции f (x) равны, то в точке a существует предельное значение этой функции, равное указанным односторонним предельным значениям) следует, что $ 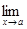f (x) = f (а), а это и означает, что f (x) непрерывна в точке а.