Инвариантность формы первого дифференциала.
Пусть y = f(x), где х - независимая переменная. Тогда оп определению dy = f'(x)dx (1) Где dx = Dx. dy называется также первым дифференциалом функции. Покажем, что формула (1) сохраняется и в том случае, когда х является не независимой переменной, а дифференцируемой функцией x = j(x), t - независимая переменная. y = f(j(t)) º F(t), dy = F'(t)dt. Воспользуемся формулой дифференцирования сложной функции:
F'(t) = f'(j(t))j'(t).
dy = f'(j(t))j'(t)dt.
Но, так как x = j(t), то dx = j'(t)dt, dy = f'(x)dx, то есть формула 1 остается в силе и в этом случае. Это свойство называется инвариантностью формы первого дифференциала. Отметим, что не меняется только форма (вид) первого дифференциала, а содержание меняется. Именно, если х - независимая переменная, то dx = Dx, если же x = j(t), то dy = j'(t)dt ¹Dx.
Из формулы (1) получаем, что f'(x) = 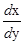 , (2) то есть производная функции f(x) равна отношению дифференциалов функции и аргумента также и в том случае, когда аргумент является не независимой переменной, а дифференцируемой функцией какой-то независимой переменной.
, (2) то есть производная функции f(x) равна отношению дифференциалов функции и аргумента также и в том случае, когда аргумент является не независимой переменной, а дифференцируемой функцией какой-то независимой переменной.
В качестве следствия из формулы (2) выведем формулу производной функции, заданной параметрически.
Пусть x и y заданы как функции независимой переменной t, которую мы назовём параметром.
x = j(t), y = y(t) (3)
пусть параметр t также изменяется на некотором промежутке и пусть t = j-1(x). Таким образом, уравнения (3) задают функцию f(x). Такое задание функции называется параметрическим. Выведем формулу f'(x). По формуле (2): f'(x)= 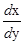 , но dy=y'(t)dt, dx=j'(t)dt Þ f'(x) =
, но dy=y'(t)dt, dx=j'(t)dt Þ f'(x) = 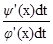 .
.
f'(x) = 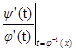 (4)
(4)
Уравнение (3) и формула (4) допускают простую физическую интерпретацию. Пусть t -время, (x, y)- координаты точки. Тогда уравнения (3) задают движение точки на плоскости, при это график y = j(x) является траекторией точки.
(рисунок)
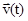 = j(t)
= j(t) 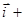 y(t)
y(t) 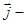 вектор скорости. Докажем, что этот вектор направлен по касательной к траектории. В самом деле, tg a =
вектор скорости. Докажем, что этот вектор направлен по касательной к траектории. В самом деле, tg a = 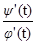 .
. 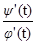 = f'(x) Þ tga = f'(x). А это и означает, что вектор скорости направлен по касательной.
= f'(x) Þ tga = f'(x). А это и означает, что вектор скорости направлен по касательной.
Пример: x = cos t (cos t есть j(t)), y = sin t (sin t есть y(t)), 0 < t < p.. Функция x = cos t имеет обратную: t = arccos x, и эти уравнения задают параметричскую функцию y = f(x). По формуле (4): f'(x) = 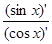 =
= 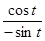 (0 < t < p).
(0 < t < p).
1) f'(x) = 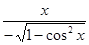 =
= 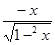 .
.
2) В данном случае f(x) можно найти в явном виде:
y = sin(arccos x) = 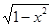 (
(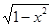 есть f(x))
есть f(x))
f'(x) = 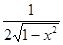 (-2x) =
(-2x) = 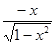 .
.
 2015-04-20
2015-04-20 3055
3055
