Замена переменной в неопределенном интеграле. Теорема 5.2. Пусть функция x=j(t) определена и дифференцируема на промежутке T, и пусть промежуток X - множество ее значений

Замена переменной.

Теорема 5.2. Пусть функция x = j (t) определена и дифференцируема на промежутке T, и пусть промежуток X - множество ее значений. Пусть f (x) определена на X и имеет первообразную F (x).

Тогда F (j (t)) - первообразная для f (j (t)× j' (t) на T.

Доказательство.

" t Î T: F (j (t))' = 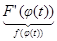× j' (t) = f (j (t)× j' (t).

Теорема доказана.

Следствие. 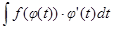= F (j (t)) + С.

F (j (t)) + С = = .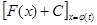

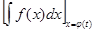Таким образом, 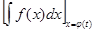= 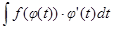-- формула замены переменной в неопределенном интеграле.

Примеры:

1) 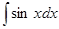= [ x = 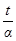,dx = 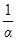dt ] =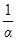 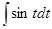= 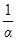(- cos t + C) = 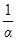cos ax + C.

2) 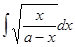, (a > 0)

Подынтегральная функция определена для 0 £ x £ a.

x = a sin² t (a sin² t º j (t)), 0 £ t £ 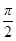, dx = 2 a sin t cos tdt

sin t = 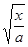, t = arcsin 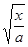, cos t = .

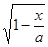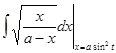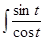= 2 a sin t cos tdt 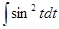= 2 a = 2 a =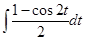

= a (t - 1/2sin2 t) + C = a (t - sin t cos t) + C = a arcsin 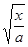- 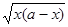+ C.

Интегрирование по частям в неопределенном интеграле.