2015-04-20
1028
Из Теоремы 13.1 можно извлечь два важных следствия.
Следствие 1. Если ряд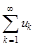 
сходится, то последовательность 
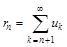является бесконечно малой.
Доказательство. Достаточно доказать, что для "e > 0 найдется номер N такой, что для всех n ³ N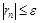 
. Это неравенство непосредственно вытекает из неравенства (2), справедливого для любого p = 1, 2, 3,…, и из Теоремы 3.13.
Следствие 2. (необходимое условие сходимости ряда). Для сходимости ряда 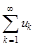необходимо, чтобы последовательность 
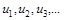членов этого ряда являлась бесконечно малой (
).
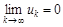Доказательство. Достаточно доказать, что для данного сходящегося ряда и для "e > 0 найдется номер N0 такой, что при n ³ N0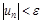 
.
Пусть дано "e > 0. По Теореме 13.1 найдется номер N такой, что при n ³ N и для любого натурального p выполняется неравенство (2). В частности, при p = 1
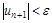(при 
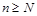) (3)
Если теперь взять номер N0 равным N0 = N + 1, то при n ³ N0 в силу (3) получим 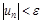, что и требовалось доказать.
