Определение производной вектор-функции

Если каждому числу t из некоторого множества T поставлен в соответствие вектор 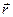, то говорят, что на множестве T, определена векторная функция (или вектор - функция) и пишут: 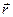= 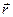(t), t Î T. | 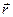(t) | - скалярная функция.

Определение. Вектор 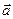называется пределом вектор-функции 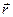= 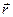(t) при t ® t₀ если | 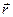(t) - 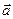| ® 0 при t ®t₀,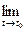 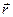(t) = .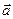

Зафиксируем какое-нибудь значение t, а затем дадим приращение Dt ¹ 0 аргументу t. D 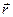= 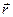(t + D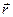t) - (t)

Определение производной вектор-функции. Если существует 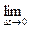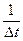D 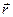, то он называется производной вектор-функции в точке t и обозначается D 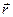'(t).