С5. Найдите все значения параметра а, при каждом из которых имеет единственное решение (x;y) система уравнений

А 0 2

Только при а<0 отрезок [0;2] является решением второго неравенства

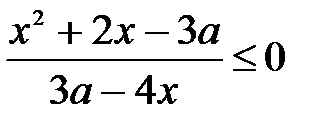
При a < 0 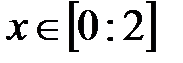3a-4x < 0

Значит числитель дроби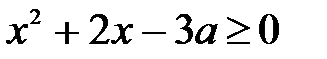

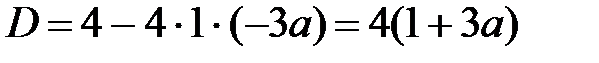
Если D<0 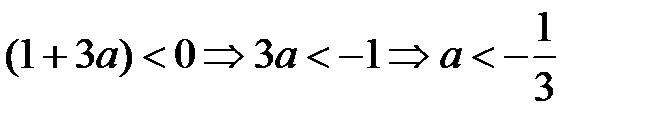, то квадратичное неравенство 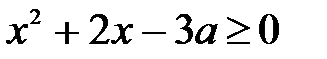(а > 0 D < 0) выполняется при всех x

При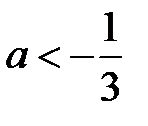

В данном неравенстве решение будем помечать «синим цветом»

3/4a 0

При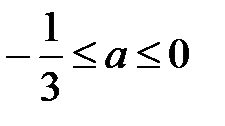

Корни квадратного трехчлена, стоящего в знаменателе

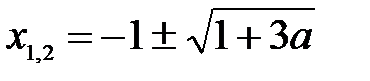
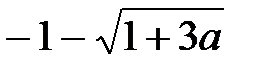
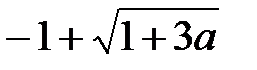3/4а 2

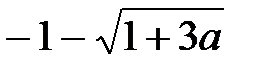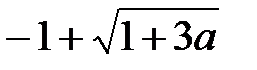О расположении чисел 3/4а при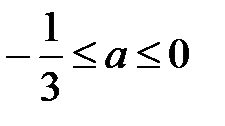

Можно доказать или «прикинуть»

Теперь совместим решения первого и второго неравенства, для получения неравенства системы

При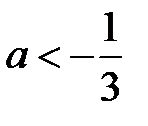

А 0 2

3/4a 0

Общим решением системы является Отрезок [0;2]

При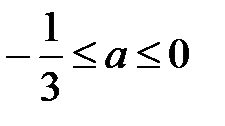

¾ а 0 2

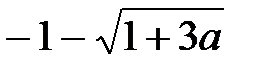
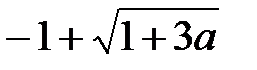3/4a 0 2

Общим решением системы будет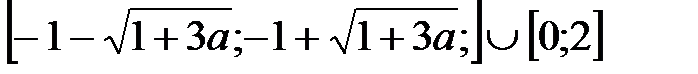

Обобщим исследование

K – решение исходного неравенства

При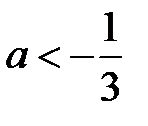

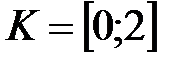
При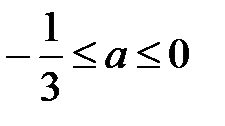

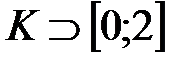
Ответ: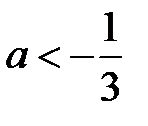

В последнем варианте было предложено следующее задание:

С чего начали тем и закончили. А то что было в середине рассмотрено далее.

С5. Найдите все значения параметра а, при каждом из которых множеством решений неравенства 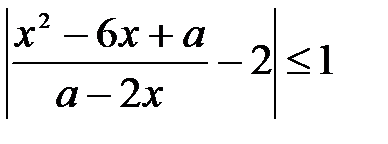справедливо при всех значениях x из отрезка [0;1].

В чем разница с первой задачей. Не только в самом неравенстве и отрезке, но и в вопросе задаче. При переводе с русского языка на язык математики.

Найти все значения a, множество решений нашего неравенства K «шире» чем отрезок [0;1] или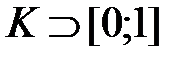

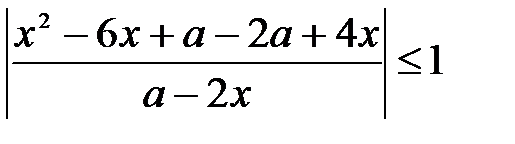
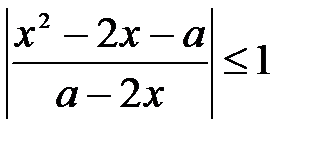
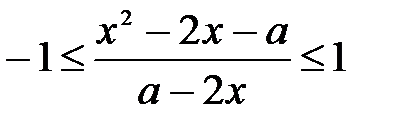
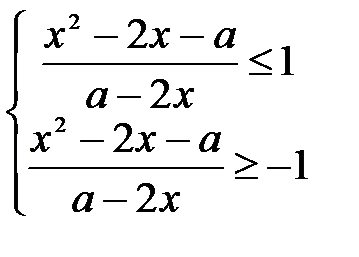
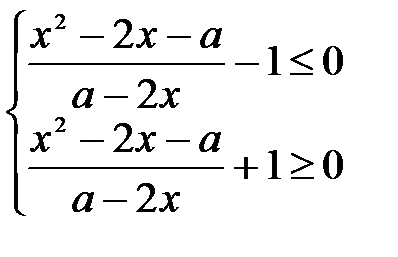
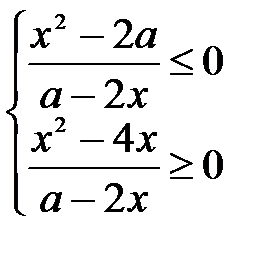
Решим второе неравенство методом интервалов

Корни числителя и знаменателя x=0; x=4 x=1/2 а

Если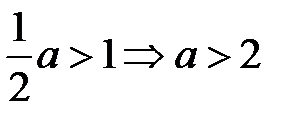

Красными отрезками отметим решение неравенства

0 1 1/2а 4

Если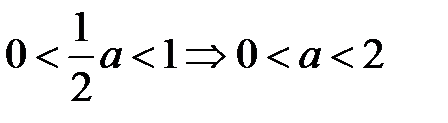

Красными отрезками отметим решение неравенства

0 1/2а 1 4

Если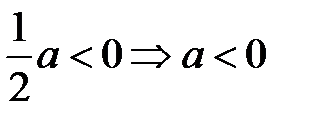

Красными отрезками отметим решение неравенства

А 0 4

Только при а<0 неравенство справедливо при всех значениях x из отрезка [0;1]

Первое неравенство 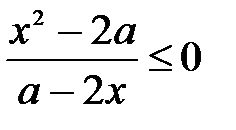рассмотрим только при а <0

Неравенство 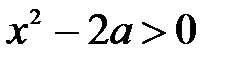при a<0 при всех х верно

Тогда a- 2x < 0

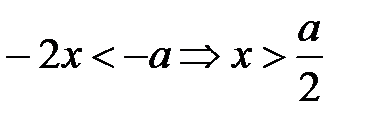является решением неравенства

1/2a 0

Отрезок [0;1] при a<0 входит в решение первого неравенства

Ответ: a<0

С5. Найдите все значения параметра а, при каждом из которых имеет единственное решение (x;y) система уравнений

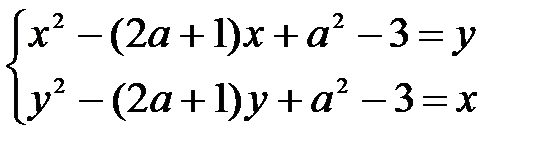
После того как «набил» первое уравнение системы, я его скопировал во второе уравнение и x заменил на у и у заменил на х.

Если система имеет решение (x₀;y₀) и x₀ ¹ y₀ тогда она будет иметь и решение (y₀;x₀) в силу симметричности уравнений.

Если система имеет единственное решение, то x₀ = y₀

Тогда любое из уравнений будет иметь вид

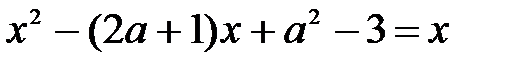
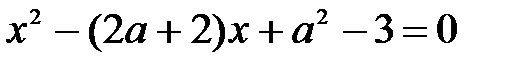
Чтобы данное уравнение имело единственное решение

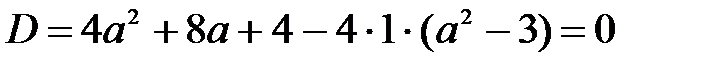
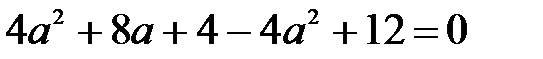
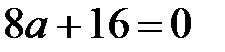
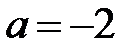
Ответ: a = -2