2015-04-23
6166
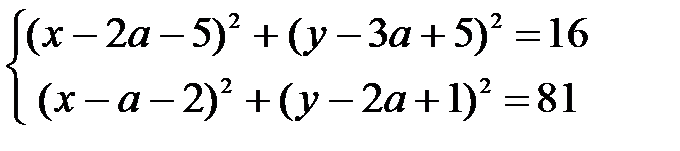
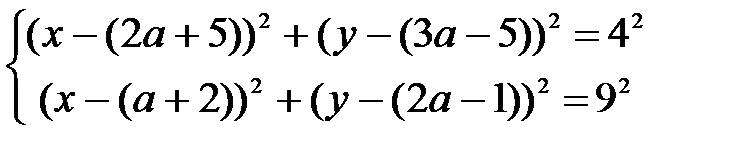
Каждое уравнение системы – это уравнение окружности
Первое – это уравнение окружности с центром (2a+5;3a - 5) и R=4
Второе - это уравнение окружности с центром (a+2;2a - 1) и R=9
Две окружности имеют одну общую точку (решение системы), когда они касаются внешним или внутренним образом.
Если касаются внешним образом, то расстояние между центрами будем
равно d=4+9=13
| R1 |
| R2 |
Квадрат расстояния между двумя точками
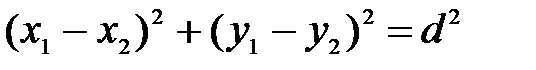
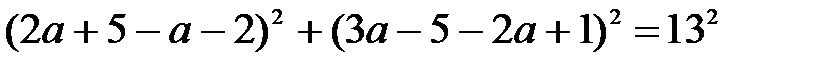
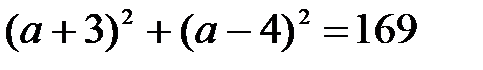
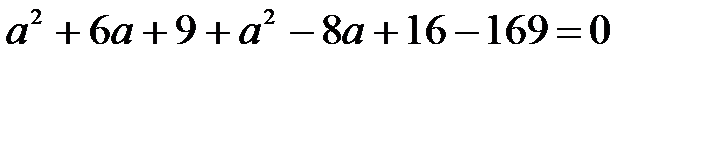
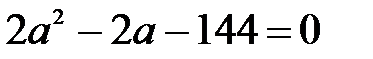(; 2)
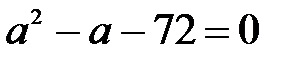
Решая квадратное уравнение, получаем
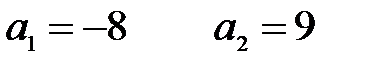
При касании внутренним образом
d = 9-4=5
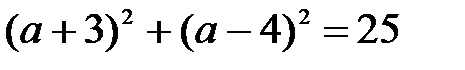
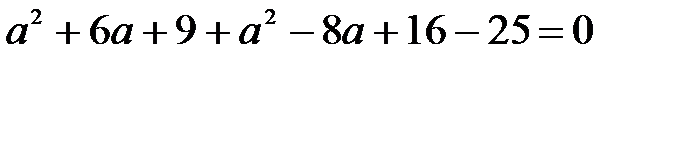
| R2 |
| R1 |
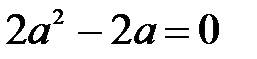
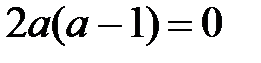
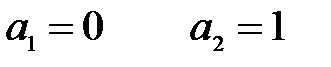
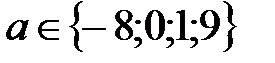
С5. Найдите все значения параметра а, при каждом из которых уравнение
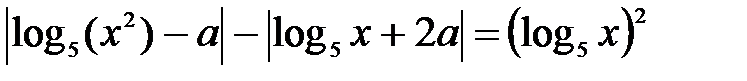имеет ровно четыре решения
Так как область определения x > 0, то выполнено будет тождество для x > 0
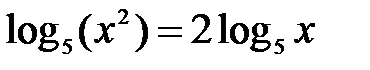
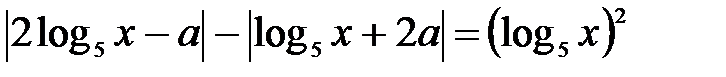
Сделаем замену переменной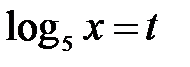 
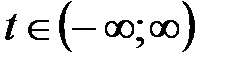
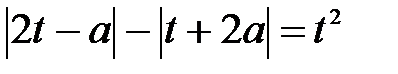
Будем рассматривать две функции
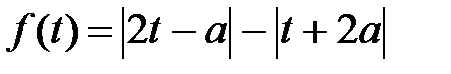левая часть уравнения
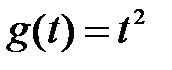правая часть уравнения
Рассмотрим случаи a > 0, a<0 и a=0
1) a>0
Построим график функции f(t)
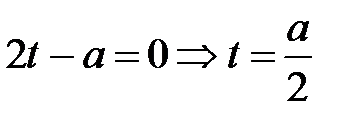
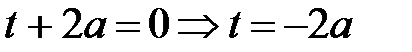
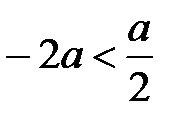для a>0
Для t рассмотрим промежутки
А)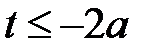 
Б)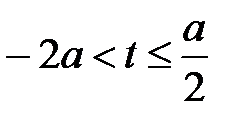 
В)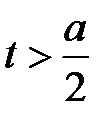 
А)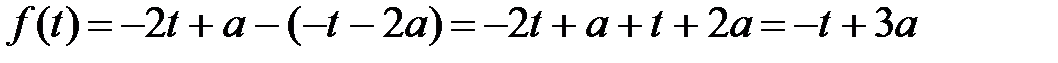 
Б)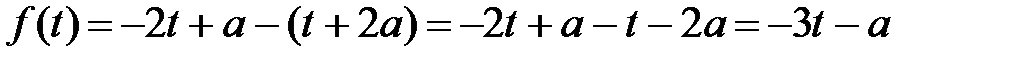 
В)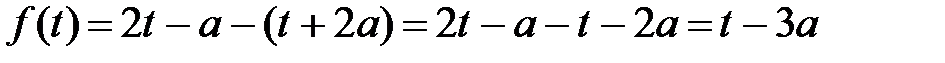 
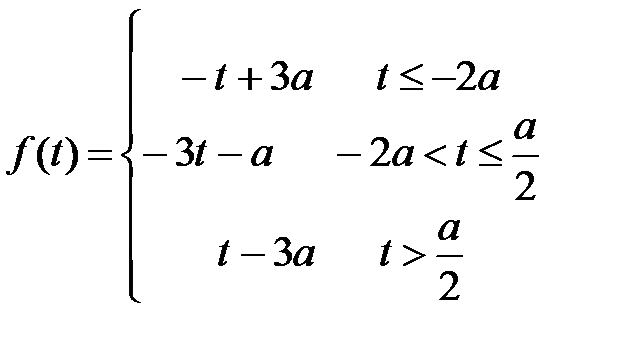
Графиком функции будет ломаная линия, состоящая из двух луче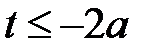й
( и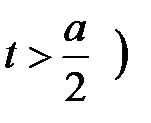 
и отрезка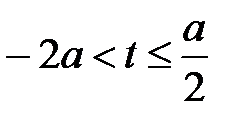
Вершины данной линии, при различных а, будут лежать
на прямых: для вершины соединяющей луч 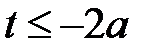и отрезок
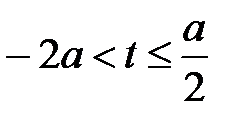в точке с координатами (-2а; 5а)
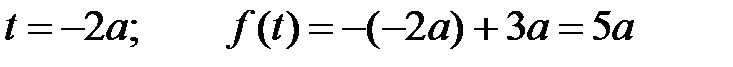
Уравнение прямой будет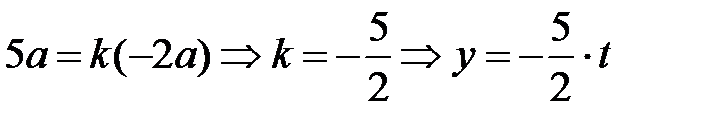 
(синяя пунктирная линия)
для вершины соединяющей луч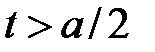 
и отрезок
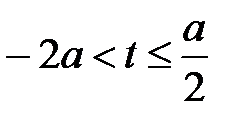в точке с координатами (а/2; -3/2а)
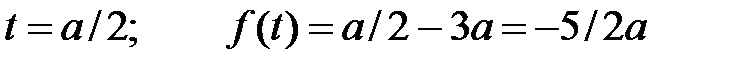
Уравнение прямой будет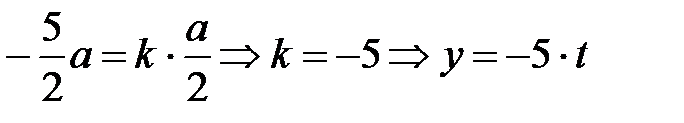 
(черная пунктирная линия)
График функции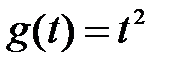 
будет известная всем, кто читает этот материал, парабола.
По графику видно, что уравнение будет иметь 4 корня когда
Прямая f(t)=t-3a будет пересекать параболу в двух точках
Уравнение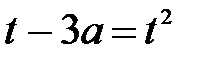 
имеет два корня
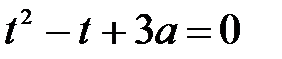
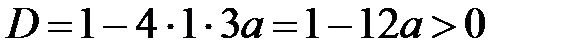
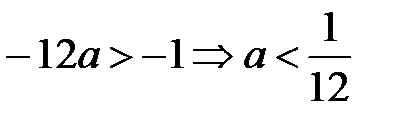
С учетом условия, что мы рассматриваем случай a>0
Получаем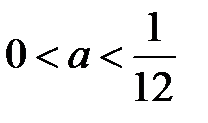 
2) a < 0
Построим график функции f(t) для a<0
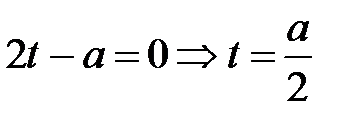
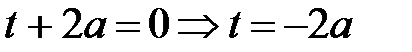
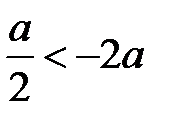для a < 0
Для t рассмотрим промежутки
А)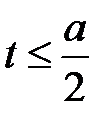 
Б) 
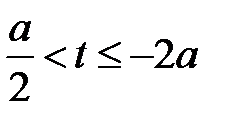В)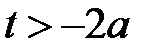 
А)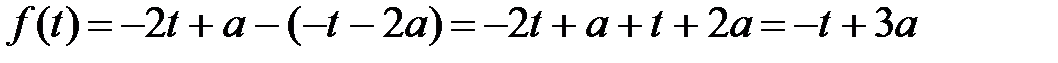
Б)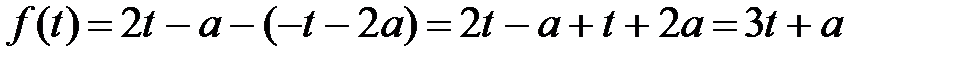 
В)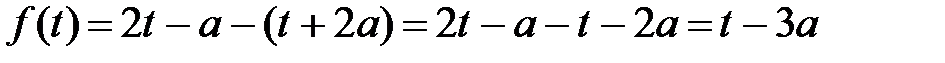
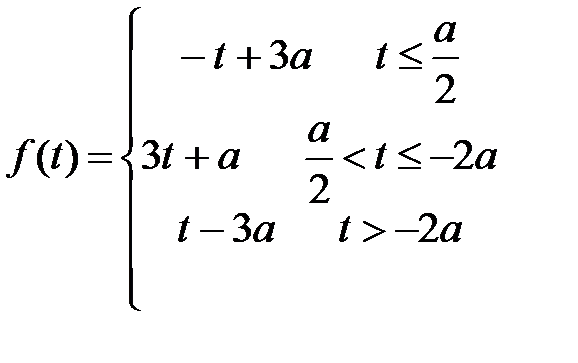
для вершины соединяющей луч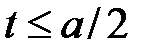 
и отрезок
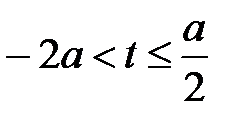в точке с координатами (а/2; 5/2а)
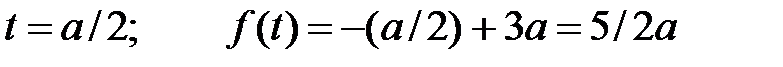
Уравнение прямой будет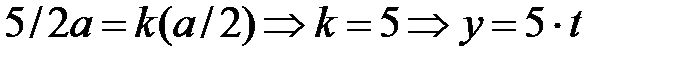 
(синяя пунктирная линия)
для вершины соединяющей луч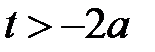 
и отрезок
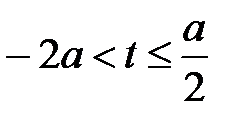в точке с координатами (-2а; -5а)
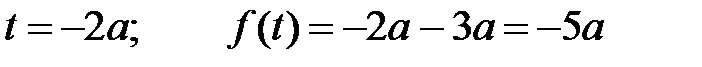
Уравнение прямой будет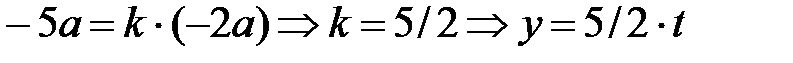 
(черная пунктирная линия)
По графику видно, что уравнение будет иметь 4 корня когда
Прямая f(t)=-t+3a будет пересекать параболу в двух точках
Уравнение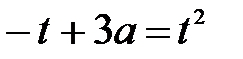 
имеет два корня
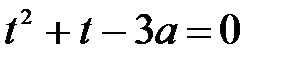
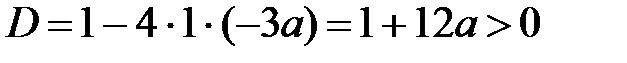
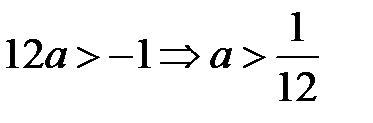
С учетом условия, что мы рассматриваем случай a<0
Получаем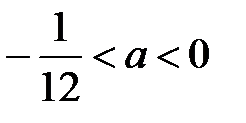 
3) a = 0
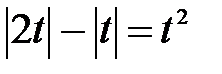
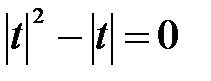
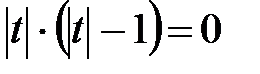
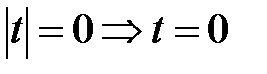
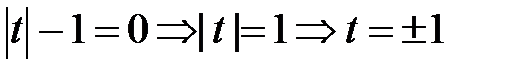
Только 3 корня
Ответ: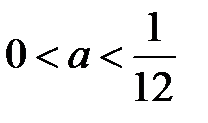
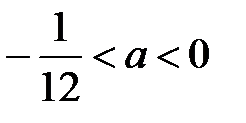
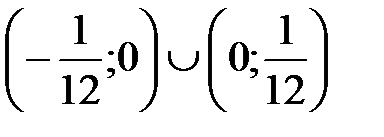
В пособиях приведено много задач подобной данной:
рассмотрим некоторые из них
