2015-04-23
1563
Рассмотрим двумерную СВ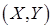 
, множество возможных значений которой 
.
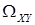О. Функцией распределения системы двух случайных величин 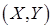называется вероятность появления события 
:
.
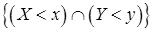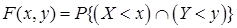Событие в фигурных скобках означает произведение событи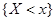й 
и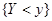 
.
Геометрическое истолкование функции распределения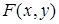 
– это вероятность попадания случайной точки 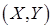в бесконечный квадрант с вершиной в точке 
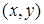, лежащей левее и ниже этой точки (см. рис. 2.1). Правая и верхняя границы в квадрант не включаются.
Из приведенной геометрической интерпретации можно вывести основные свойства функции распределения системы двух случайных величин:
1) Значения функции распределения удовлетворяют неравенству:
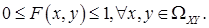
2) Функция распределения 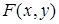есть неубывающая функция обоих своих аргументов, т.е.
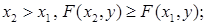при 
при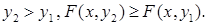 
На рис. 2.1 видно, что при увеличени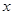и 
или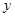 
заштрихованная зона возрастает.
3) Для функции распределения имеют место предельные соотношения:
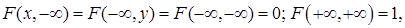
т.е.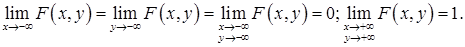 
4) Если один из аргументов стремится к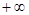 
, то функция распределения 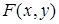становится равной функции распределения случайной величины, соответствующей другому аргументу:
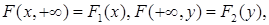
где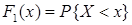 
– функция распределения СВ 
; 
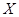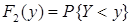– функция распределения СВ 
.
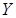В этом случае квадрант превращается в полуплоскость, вероятность попадания в которую есть функция распределения случайной величины, соответствующей другому аргументу.
5) Функции распределения 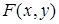непрерывна слева по каждому аргументу.
Знание функции распределения 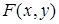позволяет решить задачу о вычислении вероятности попадания случайной точки 
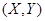в любые прямоугольные области.
Т.1. Вероятность попадания случайной точки в бесконечную полуполосу равна приращению функции распределения по одному из аргументов:
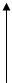у 
.
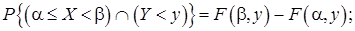
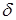
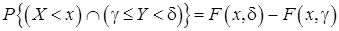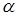
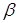х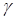 
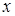
Т.2. Вероятность попадания случайной точки в прямоугольник равна:
.
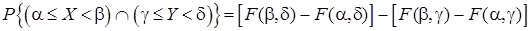Функции распределения 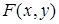– наиболее универсальная форма закона распределения, пригодная как для дискретных, так и непрерывных случайных величин.
