Решение обратной задачи – отыскание закона распределения системы по законам распределения, входящих в систему случайных величин, в общем случае невозможно.
В частном случае, когда случайные величины независимы, задача решается достаточно просто.
О.1. Две случайные величины 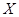 и
и 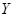 называются независимыми, если независимы все связанные с ними события:
называются независимыми, если независимы все связанные с ними события: 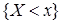 и
и 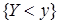 ,
, 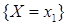 и
и  , и т.д.
, и т.д.
Кроме того, две случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина.
Т.1. Для того, чтобы СВ Х и Y, входящие в двумерную СВ 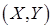 , были независимы, необходимо и достаточно, чтобы функция распределения системы
, были независимы, необходимо и достаточно, чтобы функция распределения системы 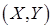 была равна произведению функций распределения ее составляющих:
была равна произведению функций распределения ее составляющих:
 .
.
Т.2. Для того, чтобы ДСВ Х и Y, входящие в двумерную СВ 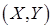 , были независимы, необходимо и достаточно, чтобы выполнялось равенство:
, были независимы, необходимо и достаточно, чтобы выполнялось равенство:
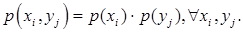
Для зависимых случайных величин вводится понятие об условном законе распределения.
О.2. Условным законом распределения (условным распределением) СВ 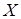 , входящей в систему
, входящей в систему 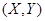 , называется ее закон распределения, вычисленный при условии, что другая случайная величина приняла определенное значение.
, называется ее закон распределения, вычисленный при условии, что другая случайная величина приняла определенное значение.
Для дискретной двумерной СВ 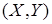 условие распределения составляющей Х при условии, что
условие распределения составляющей Х при условии, что 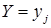 , имеет вид:
, имеет вид:
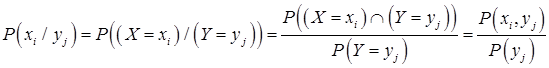 .
.
 2015-04-23
2015-04-23 1353
1353
