Рассмотрим двумерную дискретную СВ 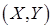 , т.е. величину составляющие которой дискретны и определены на одном и том же пространстве элементарных событий
, т.е. величину составляющие которой дискретны и определены на одном и том же пространстве элементарных событий 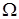 . Множество значений
. Множество значений 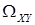 такой СВ содержит конечное или счетное число точек
такой СВ содержит конечное или счетное число точек 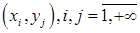 .
.
Тогда вероятность любого события  удовлетворяет аксиомам Колмогорова:
удовлетворяет аксиомам Колмогорова:
· 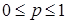 ,
,
·  ,
,
· 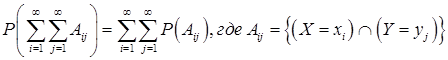 .
.
О. Матрицей (таблицей) распределения дискретной двумерной СВ 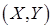 называют перечень возможных значений этой величины (т.е. пар чисел
называют перечень возможных значений этой величины (т.е. пар чисел 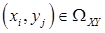 ) и их вероятностей
) и их вероятностей 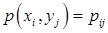 , характеризующих вероятность того, что составляющая Х примет значение
, характеризующих вероятность того, что составляющая Х примет значение 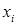 одновременно с этим составляющая Y примет значение
одновременно с этим составляющая Y примет значение 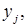
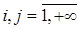 .
.
Построим матрицу распределения – прямоугольную таблицу, в которой записаны все вероятности 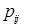 (первая строка содержит все значения СВ Х, вторая – Y):
(первая строка содержит все значения СВ Х, вторая – Y):
| Х Y | 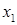 | 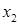 | ... | 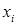 | ... |
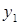 | 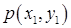 | 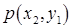 | ... | 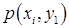 | ... |
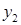 | 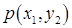 | 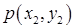 | ... | 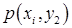 | ... |
| ... | ... | ... | ... | ... | ... |
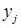 | 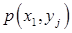 | 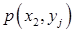 | ... | 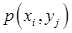 | ... |
| ... | ... | ... | ... | ... | ... |
Сумма все вероятностей матрицы распределения равна единице:
 .
.
При наличии матрицы распределения системы двух дискретных случайных величин 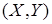 ее функция распределения находится суммированием всех вероятностей
ее функция распределения находится суммированием всех вероятностей 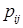 , для которых
, для которых 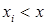 и
и  , т.е.
, т.е.
 .
.
По матрице распределения системы 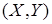 можно найти законы (ряды) распределения отдельных случайных величин
можно найти законы (ряды) распределения отдельных случайных величин 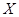 и
и 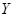 .
.
Событие 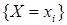 представим как сумму несовместных вариантов:
представим как сумму несовместных вариантов:
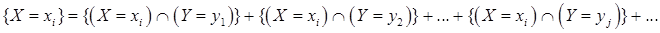
Просуммировав соответствующие вероятности, окончательно получаем:
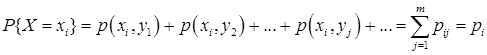 .
.
Ряд распределения составляющей Х:
| Х | 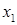 | 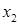 | ... | 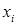 | ... |
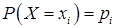 |  | 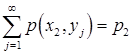 | ... | 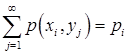 | ... |
Аналогично получаем:
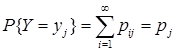 .
.
Ряд распределения составляющей Y:
| Y | 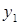 | 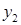 | ... | 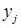 | ... |
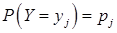 | 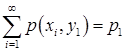 | 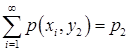 | ... | 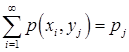 | ... |
Т.о., чтобы найти вероятность того, что отдельная случайная величина, входящая в систему, примет определенное значение, надо просуммировать вероятности 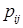 , стоящие в соответствующей этому значению строке (столбце) матрицы распределения.
, стоящие в соответствующей этому значению строке (столбце) матрицы распределения.
Пример. Передаются два сообщения, каждое из которых может быть независимо от другого принято с искажением или без искажения. Вероятность того, что первое (второе) сообщение принято с искажением, равна 0,1 (0,15). Составить матрицу распределения двумерной СВ 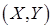 и функцию распределения
и функцию распределения  , если
, если
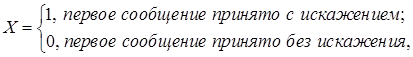
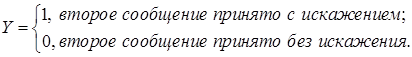
 2015-04-23
2015-04-23 1031
1031
