2015-04-23
1553
Распределение вероятностей двумерной СВ (X,Y) полностью ее характеризует. Но иногда достаточно знать лишь некоторые числовые характеристики, описывающие особенности математической модели эксперимента.
Рассмотрим начальные и центральные моменты двумерной СВ.
О.1. Начальным моментом порядка k+s двумерной СВ (X,Y) называется математическое ожидание произведения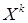 
и 
:
.
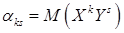О.2. Центральным моментом порядка k+s двумерной СВ (X,Y) называется математическое ожидание произведения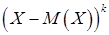 
и 
:
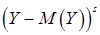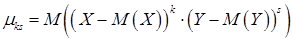или
,
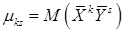где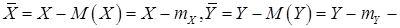 
центрированные СВ.
Для системы дискретных случайных величин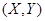 
:
; 
.
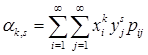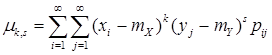Порядок моментов определяется суммой индексов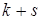 
.
Начальные моменты первого порядка – это математические ожидания случайных величин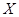 
и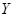 
:
; 
.
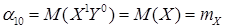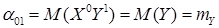Отметим, что точка 
представляет собой характеристику положения случайной точки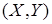 
, и разброс возможных значений системы случайных величин происходит вокруг этой точки.
Центральные моменты первого порядка равны нулю: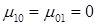 
.
Центральные моменты второго порядка:
1) Первые два центральных момента – это дисперсии случайных величин 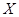и .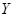
;
;
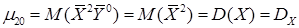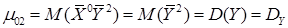2) О.3. Момент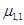 
называется смешанным центральным моментом второго порядка или ковариацией (корреляционным моментом или моментом связи) и обычно обозначается как 
:
.
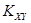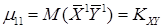Свойства ковариации:
1) Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий этих величин:
,
.
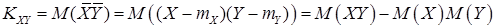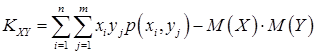2) 
.
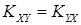3) Дисперсию можно рассматривать как частный случай ковариации, т.е.:
, 
.
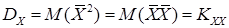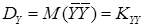4) Ковариация двух независимых случайных величин Х и Y, входящих в двумерную СВ (X,Y), равна нулю: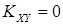 
.
5) Ковариация характеризует степень зависимости случайных величин и их рассеивание вокруг точки .
6) Размерность ковариации, так же как и дисперсии, равна квадрату размерности случайной величины.
Степень зависимости случайных величин 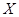и 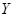удобнее характеризовать посредством безразмерной величины – коэффициента корреляции:
О.4. Коэффициентом корреляции СВ 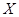и 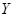, входящих в двумерную СВ (X,Y), называют отношение ковариации к произведению средних квадратических отклонений этих величин:
.
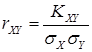Свойства коэффициента корреляции:
1) 
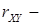безразмерная величина;
2) 
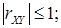
3) Если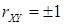 
, то между составляющими 
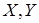существует линейная функциональная зависимость: 
, 
(
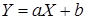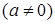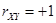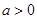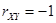при 
; 
при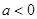 
).
4) Коэффициент корреляции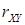 
независимых СВ равен нулю, т.к. .
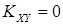О.5. СВ 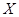и 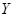, для которых 
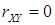, называют некоррелированными.
Замечание. Две независимые СВ всегда не коррелированы, но некоррелированные СВ не всегда являются независимыми. Равенство нулю 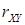является необходимым, но не достаточным условием независимости СВ.
5) Если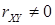 
, то составляющие 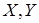зависимы.
6) Если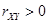 
, то говорят, что случайные величины 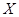, 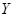связаны положительной корреляцией (т.е. при возрастании одной из случайных величин другая также проявляет тенденцию в среднем возрастать); при 
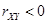– отрицательная корреляция между случайными величинами (т.е. при возрастании одной из случайных величин другая в среднем убывает).
