Балансовая модель производства является одной из наиболее простых моделей. Она записывается в виде системы уравнений, каждое из которых выражает требование равенства (баланса) между производимым отдельным экономическим объектом количеством продукции и совокупной потребностью в этой продукции. Балансовая модель хорошо отражает многие существенные особенности современного производства и в то же время легко рассчитывается на ЭВМ. При балансовых исследованиях используется аппарат линейной алгебры.
Пусть экономическая система состоит из n экономически взаимосвязанных объектов. Продукция каждого объекта (валовый выпуск) частично идет на внешнее потребление (конечный продукт), а частично используется объектами данной экономической системы. Эта часть продукции называется производственным потреблением. Таким образом, каждый объект системы выступает и как производитель продукции, и как ее потребитель.
Введем следующие обозначения:
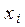 - валовый выпуск продукции i -го объекта за планируемый период;
- валовый выпуск продукции i -го объекта за планируемый период;
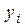 - конечный продукт i -го объекта, идущий на внешнее потребление;
- конечный продукт i -го объекта, идущий на внешнее потребление;
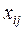 -часть продукции i -го объекта, которая потребляется
-часть продукции i -го объекта, которая потребляется 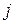 -м объектом для обеспечения выпуска его продукции в размере
-м объектом для обеспечения выпуска его продукции в размере 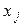 .
.
В дальнейшем будем полагать, что баланс составляется не в натуральном, а в стоимостном измерении.
Для рассматриваемой экономической системы величины 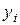 выступают в виде планового задания. Составить план для данной экономической системы – это значит на основании набора n чисел заданий указать
выступают в виде планового задания. Составить план для данной экономической системы – это значит на основании набора n чисел заданий указать 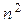 чисел
чисел 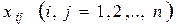 .
.
Таблица 2.1 представляет собой балансовую таблицу.
Очевидно, величины, расположенные в строках табл.2.1, связанны балансовыми равенствами
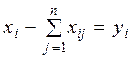 ; (
; (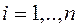 ). (2.1)
). (2.1)
Введем в рассмотрение величины 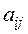 , которые называются коэффициентами прямых затрат или технологическими коэффициентами. Они определяют расход продукции i -го объекта на выпуск единицы продукции
, которые называются коэффициентами прямых затрат или технологическими коэффициентами. Они определяют расход продукции i -го объекта на выпуск единицы продукции 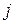 -го объекта. Тогда справедливо равенство
-го объекта. Тогда справедливо равенство
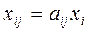 ;
; 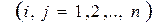 . (2.2)
. (2.2)
Таблица 2.1
Структура балансовой таблицы
| Номер объекта | Потребление | Конечный продукт | Валовый выпуск | ||||||
| ... | 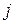 | ... | 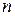 | 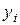 | 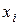 | ||||
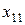 | 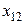 | ... | 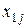 | ... | 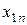 | 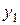 | 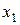 | ||
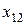 | 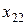 | ... | 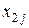 | ... | 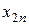 | 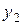 | 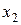 | ||
| Произ- | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| водство | 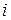 | 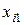 | 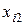 | ... | 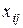 | ... | 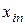 | 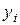 | 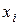 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | |
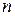 | 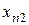 | 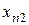 | ... | 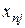 | ... | 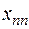 | 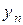 | 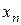 |
Приближенно можно полагать, что коэффициенты 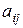 постоянны в некотором промежутке времени, охватывающем как истекший, так и планируемый периоды. Поэтому они могут быть вычислены по формуле
постоянны в некотором промежутке времени, охватывающем как истекший, так и планируемый периоды. Поэтому они могут быть вычислены по формуле 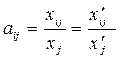 , где
, где 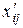 и
и 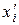 - данные, относящиеся к истекшему периоду.
- данные, относящиеся к истекшему периоду.
Пусть теперь известны коэффициенты прямых затрат для всех объектов экономической системы. Эти данные могут быть записанные в виде матрицы 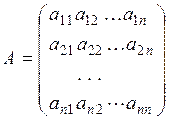 ,
,
которая называется матрицей коэффициентов прямых затрат.
Важной особенностью матрицы 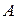 является неотрицательность ее коэффициентов, т.е.
является неотрицательность ее коэффициентов, т.е. 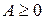 .
.
На основании выражения (2.2) систему уравнений (2.1) перепишем в виде
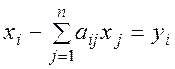 ;
; 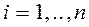 (2.3)
(2.3)
или в матричной форме 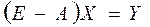 , (2.4)
, (2.4)
где 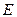 - единичная матрица n -го порядка;
- единичная матрица n -го порядка; 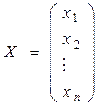 ;
; 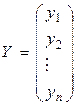 .
.
Система уравнений (2.3) представляет собой систему уравнений балансовой модели.
При решении балансовых уравнений будем исходить из заданного вектора 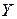 , который называется ассортиментным, и определять необходимый для его производства вектор
, который называется ассортиментным, и определять необходимый для его производства вектор 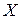 , называемый вектором-планом.
, называемый вектором-планом.
При исследовании системы (2.3) возникает вопрос о существовании при заданном векторе 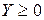 неотрицательного решения
неотрицательного решения 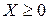 , т.е. о существовании вектора-плана, обеспечивающего данный ассортимент конечной продукции.
, т.е. о существовании вектора-плана, обеспечивающего данный ассортимент конечной продукции.
Можно доказать, что если существует хотя бы один неотрицательный вектор 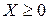 , удовлетворяющий неравенству
, удовлетворяющий неравенству 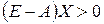 , т.е. если уравнение (2.4) имеет неотрицательное решение
, т.е. если уравнение (2.4) имеет неотрицательное решение 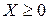 хотя бы для одного
хотя бы для одного 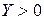 , то оно имеет для любого
, то оно имеет для любого 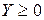 единственное неотрицательное решение. То есть, если для предшествующего периода равенство (2.4) выполняется, где
единственное неотрицательное решение. То есть, если для предшествующего периода равенство (2.4) выполняется, где 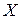 и
и 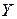 определяются по исполненному балансу за прошлые период, при этом
определяются по исполненному балансу за прошлые период, при этом 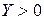 , то оно всегда имеет допустимый план и матрица
, то оно всегда имеет допустимый план и матрица 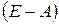 имеет обратную матрицу (неотрицательную).
имеет обратную матрицу (неотрицательную).
Обозначив обратную матрицу 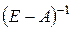 через
через 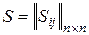 , запишем решение уравнения (2.4) в виде
, запишем решение уравнения (2.4) в виде
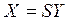 =
= 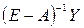 . (2.5)
. (2.5)
Таким образом, задавая ассортиментный вектор Y, по формуле (2.5) можем определить вектор-план X.
Для уяснения экономического смысла матрицы коэффициентов полных затрат рассмотрим частный вид вектора 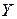 , соответствующий такому значению, при котором объект j должен выдавать одну единицу конечной продукции, а все остальные объекты выпускать конечную продукцию не должны, т.е.
, соответствующий такому значению, при котором объект j должен выдавать одну единицу конечной продукции, а все остальные объекты выпускать конечную продукцию не должны, т.е.
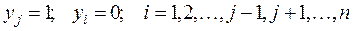 .
.
Тогда согласно формуле (2.5) получим
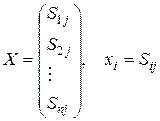 . (2.6)
. (2.6)
Соотношение (2.6) вскрывает экономический смысл элементов матрицы 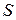 : элемент
: элемент 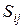 равен количеству продукции, которое должен выпустить объект i для того, чтобы объект
равен количеству продукции, которое должен выпустить объект i для того, чтобы объект 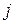 мог выпустить одну единицу конечной продукции (а не полного выпуска). В связи с этим элементы
мог выпустить одну единицу конечной продукции (а не полного выпуска). В связи с этим элементы 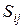 называют коэффициентами полных затрат, а матрица
называют коэффициентами полных затрат, а матрица 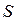 - матрицей коэффициентов полных затрат.
- матрицей коэффициентов полных затрат.
Коэффициенты полных затрат 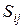 всегда не меньше, а могут быть и существенно больше соответствующих коэффициентов прямых затрат
всегда не меньше, а могут быть и существенно больше соответствующих коэффициентов прямых затрат 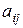 , поскольку коэффициент
, поскольку коэффициент 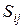 указывает не только непосредственные поставки продукции i -го объекта j -му объекту, но и поставки продукции i -го объекта другим объектам для того, чтобы эти объекты в свою очередь могли поставить j -му объекту требуемое количество их продукции.
указывает не только непосредственные поставки продукции i -го объекта j -му объекту, но и поставки продукции i -го объекта другим объектам для того, чтобы эти объекты в свою очередь могли поставить j -му объекту требуемое количество их продукции.
Для функционирования отдельных экономических объектов необходимы не только продукция других экономических объектов этой системы, но и такие факторы производства, как производственные фонды (оборудование, производственные площади и т.д.), природные ресурсы (вода, газ, лес, полезные ископаемые и т.д.), труд. Кроме этого, экономическая система может получать продукцию от других экономических систем.
Ограниченность факторов производства и поставок из других экономических систем является причиной того, что реально не всякий вектор конечной продукции может быть произведен данной экономической системой. Поэтому при планировании необходимо не только определять потоки продукции между отдельными объектами системы, но и найти потребность системы в факторах производства и поставок извне. При этом допустимым для экономической системы является такой план, при котором потребности в факторах производства и импорте не превышают соответствующих ограничений.
Рассмотрим способ определения потребности системы в факторах производства и поставок извне. При этом как факторы производства, так и импортируемые продукты будем называть факторами.
Пусть имеем 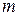 факторов. Потребность системы в факторах на планируемый период будем обозначать вектором
факторов. Потребность системы в факторах на планируемый период будем обозначать вектором 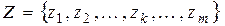 ,
,
где 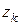 - потребность в
- потребность в 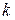 -м факторе.
-м факторе.
Потребность всех объектов в факторах может быть охарактеризована матрицей коэффициентов прямых затрат факторов:
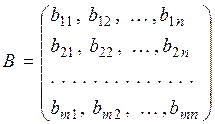 .
.
Числа 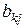 называются коэффициентами прямых затрат факторов. Коэффициент
называются коэффициентами прямых затрат факторов. Коэффициент 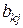 указывает, какое количество
указывает, какое количество 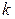 -го фактора необходимо j -му объекту для того, чтобы этот объект мог произвести одну единицу продукции.
-го фактора необходимо j -му объекту для того, чтобы этот объект мог произвести одну единицу продукции.
Если вектор полного выпуска продукции объектами системы есть 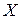 , то суммарная потребность системы в
, то суммарная потребность системы в 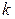 -м факторе
-м факторе 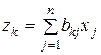 ,
, 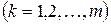 или в матричной форме
или в матричной форме
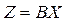 . (2.7)
. (2.7)
Вектор 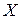 является решением системы балансовых уравнений, поэтому с учетом формы (2.5) из выражения (2.7) получим
является решением системы балансовых уравнений, поэтому с учетом формы (2.5) из выражения (2.7) получим
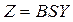 . (2.8)
. (2.8)
Соотношение (2.8) позволяет определить суммарную потребность Z в факторах для любого вектора конечной потребности 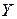 , а также установить экономический смысл матрицы
, а также установить экономический смысл матрицы 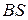 . Для этого рассмотрим частный вид вектора
. Для этого рассмотрим частный вид вектора 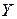 , когда
, когда 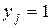 , а
, а 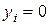 при
при 
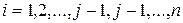 . Тогда на основании соотношения (2.8) будем иметь
. Тогда на основании соотношения (2.8) будем иметь 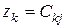

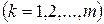 ,
,
где 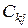

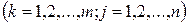 - элементы матрицы
- элементы матрицы 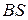 .
.
Таким образом, элемент 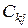 показывает, какое суммарное количество
показывает, какое суммарное количество 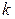 -го фактора необходимо системе для того, чтобы
-го фактора необходимо системе для того, чтобы 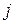 -й объект мог выпустить одну единицу конечной продукции. В связи с этим матрицу
-й объект мог выпустить одну единицу конечной продукции. В связи с этим матрицу 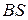 называют матрицей коэффициентов полных затрат факторов.
называют матрицей коэффициентов полных затрат факторов.
Количество каждого фактора, которое может быть использовано системой, ограничено. Это значит, что известны 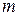 чисел
чисел 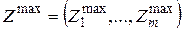 , имеющих следующий смысл: план для данной экономической системы допустим, если требуется для его реализации количество
, имеющих следующий смысл: план для данной экономической системы допустим, если требуется для его реализации количество 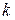 -го фактора не большее
-го фактора не большее 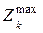 для всех
для всех 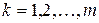 . Поэтому экономическая система может выпустить только такой вектор конечной продукции
. Поэтому экономическая система может выпустить только такой вектор конечной продукции 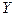 , который удовлетворяет условию
, который удовлетворяет условию 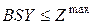 .
.
 2015-04-23
2015-04-23 4224
4224
