Одним из основных в теории потребительского выбора является уравнение Слуцкого, опубликованное российским математиком Е.Е.Слуцким в 1915 году. Это уравнение позволяет увязать действие эффекта замены и эффекта дохода с результирующим изменением спроса. Уравнение Слуцкого имеет вид:
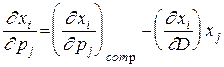 .
.
Первое слагаемое в правой части описывает действие эффекта замены, второе - действие эффекта дохода, выраженное в тех же единицах измерения (множитель 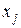 приводит их к одной размерности). Слева записано результирующее воздействие на спрос, складывающееся из изменения структуры спроса и общего его изменения при изменении уровня реального дохода. Для ценных товаров величина
приводит их к одной размерности). Слева записано результирующее воздействие на спрос, складывающееся из изменения структуры спроса и общего его изменения при изменении уровня реального дохода. Для ценных товаров величина 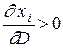 , т.е. спрос растет при росте дохода. В этом случае, согласно уравнению Слуцкого,
, т.е. спрос растет при росте дохода. В этом случае, согласно уравнению Слуцкого, 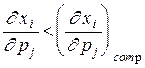 : если спрос растет, то он растет больше при наличии компенсации, если падает - то в меньшей степени. Может оказаться и так, что
: если спрос растет, то он растет больше при наличии компенсации, если падает - то в меньшей степени. Может оказаться и так, что 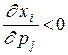 , но
, но 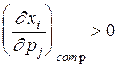 , то есть товары i и j взаимозаменяемы, но представляются взаимодополняемыми без учета компенсации.
, то есть товары i и j взаимозаменяемы, но представляются взаимодополняемыми без учета компенсации.
Уравнение Слуцкого может рассматриваться как при разных, так и при совпадающих i и j.
Из первых двух свойств функции полезности потребителя следует, что 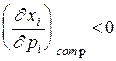 (на графике это обусловлено выпуклостью линий уровня функции полезности). Если оказывается, что
(на графике это обусловлено выпуклостью линий уровня функции полезности). Если оказывается, что 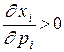 (спрос на товар растет при росте цены - такие товары называются товарами Гиффина), то отсюда вытекает, что
(спрос на товар растет при росте цены - такие товары называются товарами Гиффина), то отсюда вытекает, что 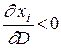 - то есть это обязательно малоценный товар.
- то есть это обязательно малоценный товар.
Проверим уравнение Слуцкого для рассмотренной выше задачи потребительского выбора с функцией полезности 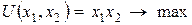 .
.
Было получено:
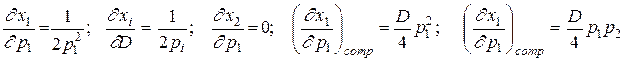
Отсюда 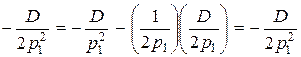 ; и
; и 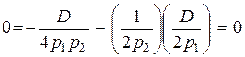 .
.
В обоих случаях уравнения Слуцкого (при i = j и при i ¹ j)здесь выполнены.
Уравнение Слуцкого может быть использовано для нахождения 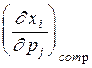 , то есть для расчета эффекта замены и оценки взаимозаменяемости или взаимодополняемости благ, поскольку частные производные без компенсации рассчитываются значительно легче.
, то есть для расчета эффекта замены и оценки взаимозаменяемости или взаимодополняемости благ, поскольку частные производные без компенсации рассчитываются значительно легче.
Рассмотрим эластичности функции спроса. Эластичность спроса по цене равна 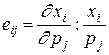 ; эластичностьспроса по доходу
; эластичностьспроса по доходу 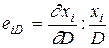 .
.
Для функции 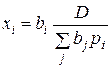 эластичность
эластичность 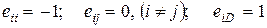 .
.
Из свойств функции спроса можно получить равенство 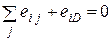 , т.е. нулю должна равняться сумма всех эластичностей спроса по ценам и доходу.
, т.е. нулю должна равняться сумма всех эластичностей спроса по ценам и доходу.
Покажем, что если в задаче потребительского выбора всего два товара, то они обязательно являются взаимозаменяемыми. Для этого воспользуемся тем, что 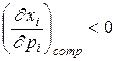 и положительностью частных производных функции полезности.
и положительностью частных производных функции полезности.
Предположим, что выросла цена 1-го товара 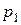 .
.
Поскольку 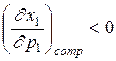 , спрос на этот товар при условии компенсации падает. Если бы при этом упал спрос и на второй товар, то мы получили бы точку, в которой обоих товаров меньше, чем в начальной.
, спрос на этот товар при условии компенсации падает. Если бы при этом упал спрос и на второй товар, то мы получили бы точку, в которой обоих товаров меньше, чем в начальной.
Следовательно, в этой точке значение функции полезности 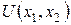 должно быть также меньше (а мы знаем, что в условиях компенсации оно равно начальному). Следовательно, спрос на второй товар при условии компенсации должен вырасти (т.е.
должно быть также меньше (а мы знаем, что в условиях компенсации оно равно начальному). Следовательно, спрос на второй товар при условии компенсации должен вырасти (т.е. 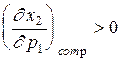 ) и он является взаимозаменяемым с первым товаром.
) и он является взаимозаменяемым с первым товаром.
Пример 10.2. На основании данных о потреблении взаимозаменяемых и взаимодополняемых продуктов x 1 и x 2 в различном сочетании i, их цене 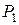 и
и 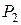 , полезности U и бюджете (доходах) потребителя D построить кривую безразличия и определить оптимальный план потребления названных продуктов.
, полезности U и бюджете (доходах) потребителя D построить кривую безразличия и определить оптимальный план потребления названных продуктов.
Исходные данные имеют вид:
| i | х 1 i | i | х 2 i |
| 2,9 | 13,5 | ||
| 3,0 | 12,0 | ||
| 5,0 | 7,5 | ||
| 7,0 | 6,0 | ||
| 10,0 | 5,0 | ||
| 12,0 | 4,5 | ||
| 12,3 | 4,6 |
U = 18; P 1 = 5; P 2 = 10,3; D = 100.
Решение. В нашей задаче продукты х1 и х 2 являются взаимозаменяемыми и взаимодополняемыми, т.е. функция смешанная. Поэтому можно воспользоваться моделью неоклассической функции полезности, которая имеет вид 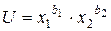 , где
, где 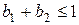 .
.
Чтобы убедиться в правильности предположения о форме связи, следует графически изобразить изучаемую зависимость в системе координат по данным о потреблении продуктов х1 и х 2. По виду графика можно предположить, что зависимость между x 1 и x 2 имеет вид 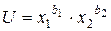 при
при 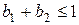 .
.
Решение задачи по построению кривой безразличия заключается в определении параметров функции b 1 и b 2. Параметры кривой безразличия b 1 и b 2 отражают степень полезности каждого из продуктов x 1 и x 2.
Определив параметры b 1 и b 2, зная одну из переменных - количество потребления продукта x 1, всегда можно определить вторую переменную x 2 так, чтобы обеспечить максимум полезности от потребления продуктов
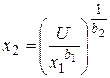 .
.
Для расчета параметров функции 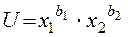 целесообразно ее линеаризовать посредством логарифмирования.
целесообразно ее линеаризовать посредством логарифмирования.
Имеем 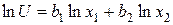 .
.
Обозначим 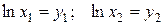 и запишем
и запишем 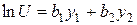 .
.
Отсюда 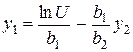 .
.
Обозначив 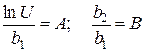 , можно записать
, можно записать 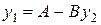 .
.
Для определения коэффициентов A и B обычно применяют метод наименьших квадратов:
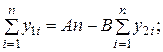
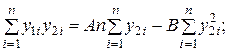
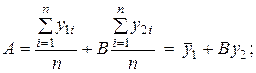
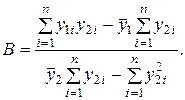
Учитывая, что 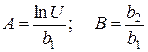 определяют
определяют 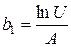 и
и 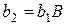 .
.
Проверяют правильность расчетов 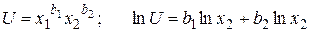 и определяют расчетную кривую безразличия
и определяют расчетную кривую безразличия 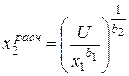 , отражающую отношения предпочтения, характерные для отдельного индивидуума.
, отражающую отношения предпочтения, характерные для отдельного индивидуума.
На графике оптимальный план потребления соответствует точке касания бюджетной прямой и кривой безразличия.
Ее координаты, т.е. значения 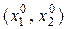 , определяются путем нахождения частных производных функций
, определяются путем нахождения частных производных функций
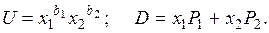
После некоторых преобразований имеем
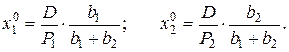
Полученные функции 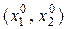 и есть функции спроса. Они отражают оптимальный размер потребления продуктов, обеспечивающий максимум полезности в рамках бюджетного ограничения при заданных ценах.
и есть функции спроса. Они отражают оптимальный размер потребления продуктов, обеспечивающий максимум полезности в рамках бюджетного ограничения при заданных ценах.
При расчете величин A и B можно воспользоваться таблицей вспомогательных расчетов.
Ниже приводятся расчеты для имеющихся данных.
Таблица 10.1
Расчет функции безразличия
| i | х 1 i | 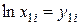 | х 2 i | 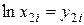 | y 1 iy2i | y2i2 |
| 2,9 | 1,065 | 13,5 | 2,603 | 2,772 | 6,776 | |
| 3,0 | 1,099 | 12,0 | 2,485 | 2,731 | 6,175 | |
| 5,0 | 1,609 | 7,5 | 2,015 | 3,242 | 4,060 | |
| 7,0 | 1,946 | 6,0 | 1,792 | 3,487 | 3,211 | |
| 10,0 | 2,303 | 5,0 | 1,609 | 3,706 | 2,589 | |
| 12,0 | 2,485 | 4,5 | 1,504 | 3,737 | 2,262 | |
| 12,3 | 2,509 | 4,6 | 1,526 | 3,829 | 2,329 | |
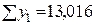 | 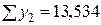 | 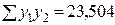 | 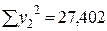 |
Определим коэффициенты A и B методом наименьших квадратов:
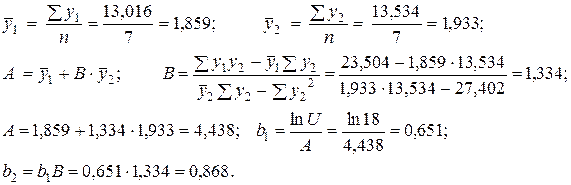
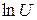 =
= 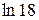 = 2.890;
= 2.890; 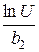 = 3.329;
= 3.329; 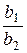 = 0.75.
= 0.75.
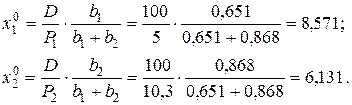
 2015-04-23
2015-04-23 3737
3737








