Пусть функция 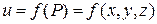 определена и непрерывна в замкнутой ограниченной области
определена и непрерывна в замкнутой ограниченной области 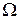 трехмерного пространства
трехмерного пространства  .
.
Разобьем область 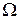 произвольным образом на n частей
произвольным образом на n частей 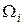 с объемами
с объемами 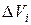
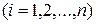 . В каждой частичной области
. В каждой частичной области 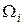 выберем произвольную точку
выберем произвольную точку 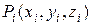 и составим сумму
и составим сумму
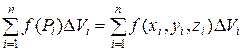 ,
,
которую назовем интегральной суммой для функции 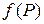 в области
в области 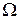 .
.
Назовем диаметром области d наибольшее расстояние между граничными точками этой области. Например, диаметром области, представляющей собой эллипсоид, будет его удвоенная наибольшая полуось.
Обозначим через 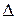 наибольший из диаметров частичных областей
наибольший из диаметров частичных областей 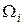 :
:
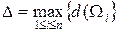 .
.
Определение. Тройным интегралом от функции 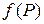 по области
по области 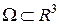 называется предел интегральных сумм при
называется предел интегральных сумм при 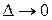 , если этот предел существует и не зависит ни от способа разбиения области
, если этот предел существует и не зависит ни от способа разбиения области 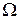 на частичные области
на частичные области 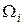 , ни от выбора в каждой из них точки
, ни от выбора в каждой из них точки 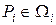 :
:
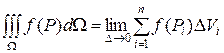
или в другой записи:
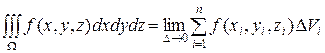 .
.
Функция 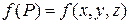 называется интегрируемой в области
называется интегрируемой в области 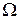 , область
, область 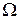 – областью интегрирования, x, y, z – переменными интегрирования,
– областью интегрирования, x, y, z – переменными интегрирования, 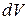 – элементом объема.
– элементом объема.
Теорема 6.2 (существования тройного интеграла) (без доказательства). Функция 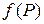 , непрерывная в замкнутой ограниченной области
, непрерывная в замкнутой ограниченной области 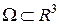 , интегрируема в этой области.
, интегрируема в этой области.
Замечание. Если положить 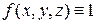 всюду в области
всюду в области 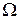 , то из определения тройного интеграла легко получить формулу для вычисления объема V области
, то из определения тройного интеграла легко получить формулу для вычисления объема V области 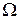 с помощью тройного интеграла
с помощью тройного интеграла
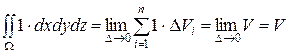
или
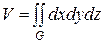 .
.
Основные свойства тройного интеграла аналогичны соответствующим свойствам двойного интеграла.
Свойство 1. Постоянный множитель можно выносить за знак интеграла:
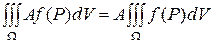 .
.
Свойство 2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:
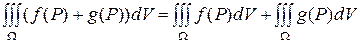 .
.
Свойство 3. Если область интегрирования 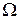 разбить на две непересекающиеся области
разбить на две непересекающиеся области 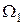 и
и 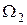 , то интеграл по всей области
, то интеграл по всей области 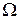 будет равен сумме интегралов по областям
будет равен сумме интегралов по областям 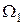 и
и 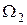 :
:
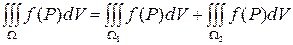 .
.
Свойство 4 (Теорема о среднем). Если функция 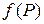 непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 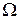 , то в этой области существует такая точка
, то в этой области существует такая точка 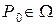 , что справедлива формула
, что справедлива формула
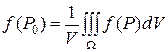 ,
,
где V – объем области 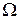 .
.
 2015-04-23
2015-04-23 2623
2623
