2015-04-23
1120
В двойном интеграле, как и в определенном, замена переменных – важнейший метод приведения интеграла к виду, более удобному для вычисления.
Наиболее важным для практических приложений частным случаем замены переменных является замена декартовых координат x и y полярными координатами – радиусом-вектором r и полярным углом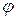 
(переход из декартовой системы координат в полярную)
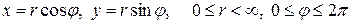
по формуле
.
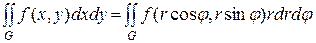Выражение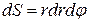 
называют обычно элементом площади в полярных координатах.
Вычисление двойного интеграла в полярных координатах, так же как и в полярных, сводится к вычислению повторного интеграла, но только роль переменных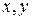 
играют теперь 
.
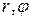Пример. Вычислить двойной интеграл
,
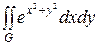где G – четверть круга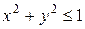 
, расположенная в первом квадранте.
Очевидно, что в области G радиус-вектор r изменяется в пределах от 0 до 1, а угол 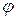– от 0 до 
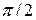(рис. 6.5).
Тогда получаем
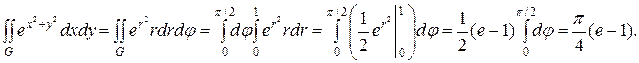
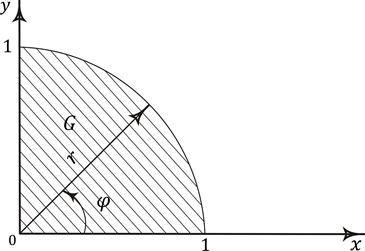
Рис. 6.5. Пример вычисления двойного интеграла в полярных координатах
