Вычисление тройного интеграла сводится к последовательному вычислению одного однократного (определенного) и одного двойного интегралов или к вычислению, в конечном итоге, трех однократных (определенных) интегралов следующим способом.
Пусть область 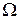 (рис. 6.6) ограничена снизу поверхностью
(рис. 6.6) ограничена снизу поверхностью 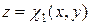 , сверху поверхностью
, сверху поверхностью 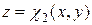 , а с боковых сторон цилиндрической поверхностью, и пусть G – проекция области
, а с боковых сторон цилиндрической поверхностью, и пусть G – проекция области 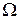 на плоскость
на плоскость 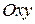 , причем всюду в области G функции
, причем всюду в области G функции 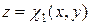 и
и 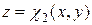 непрерывны и
непрерывны и 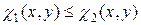 .
.
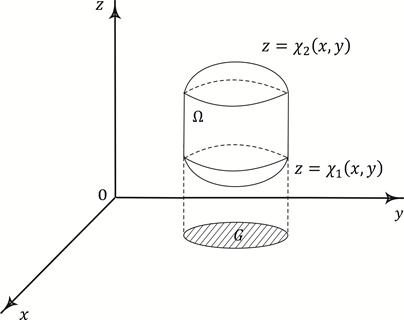
Рис.6.6. Вычисление тройного интеграла в декартовых координатах
Тогда тройной интеграл вычисляется по формуле
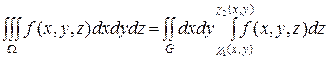 ,
,
причем сначала вычисляется внутренний определенный интеграл по переменной z (при постоянных x и y), а затем внешний двойной интеграл по области G.
Записывая двойной интеграл через один из повторных (см. п. 6.2), получаем
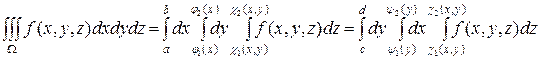 .
.
Замечание. Аналогичные формулы для вычисления тройного интеграла можно записать и для случаев проектирования области 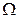 на плоскости
на плоскости 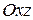 и
и 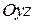 .
.
Пример. Вычислить тройной интеграл
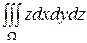 ,
,
где область интегрирования 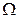 – пирамида, ограниченная плоскостью
– пирамида, ограниченная плоскостью 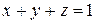 и координатными плоскостями
и координатными плоскостями 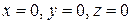 (рис. 6.7).
(рис. 6.7).
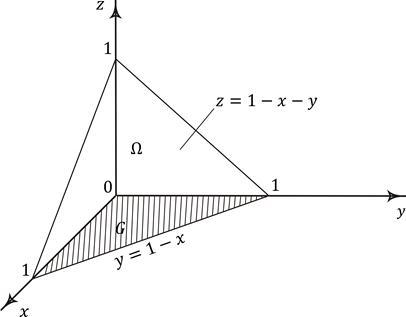
Рис. 6.7. Пример вычисления тройного интеграла в декартовых координатах
Область 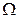 проектируется на плоскость
проектируется на плоскость 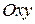 в треугольник G, ограниченный прямыми
в треугольник G, ограниченный прямыми 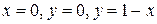 . Полагая
. Полагая
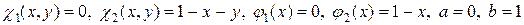
и используя сначала формулу для вычисления тройного интеграла, а затем первую формулу для вычисления двойного интеграла, получим:
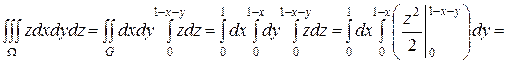

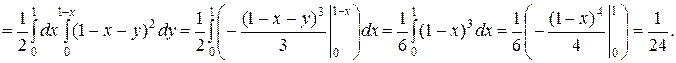
 2015-04-23
2015-04-23 1355
1355
