Вычисление двойного интеграла в декартовых координатах

Вычисление двойного интеграла сводится к вычислению двух определенных интегралов следующим способом.

Пусть область G (рис. 6.3) ограничена кривыми

,

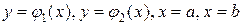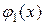причем всюду на отрезке функции и 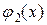непрерывны и 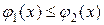. Тогда

,

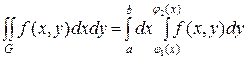причем сначала вычисляется внутренний определенный интеграл по переменной y, а полученный результат интегрируется во внешнем определенном интеграле по переменной x. При этом интеграл, стоящий в правой части формулы, называют повторным или двукратным интегралом.

Аналогично, если область G (рис. 6.3) ограничена кривыми

,

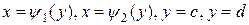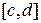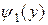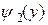причем всюду на отрезке функции и непрерывны и 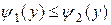, то

,

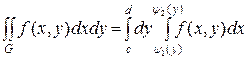причем сначала вычисляется внутренний определенный интеграл по переменной x, а полученный результат интегрируется во внешнем определенном интеграле по переменной y.

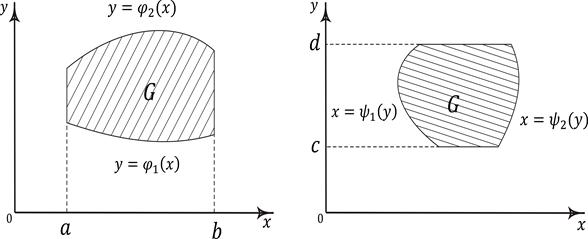
Рис. 6.3. Вычисление двойного интеграла в декартовых координатах

Пример. Вычислить двойной интеграл

,

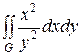если область интегрирования G ограничена линиями .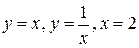

Форма области G (рис. 6.4) позволяет применить первую формулу при :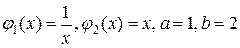

.

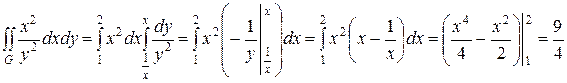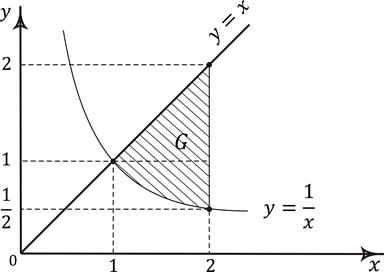
Рис. 6.4. Пример вычисления двойного интеграла в декартовых координатах

Если же для вычисления данного двойного интеграла применить вторую формулу, то следует положить

.

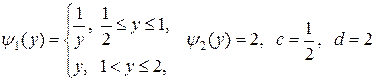Тогда, используя свойство 3 двойного интеграла, получим:

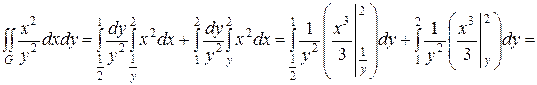
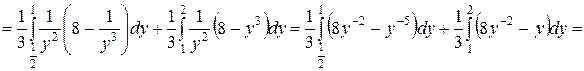
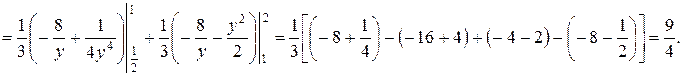
Очевидно, что в данном примере целесообразнее проводить вычисления по первой формуле.

Результаты расчетов, естественно, одинаковы.