Связь между криволинейными интегралами первого и второго рода

Обозначив через α и β углы, составляемые с осями координат Ox и Oy соответственно векторным элементом 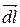касательной к кривой AB в точке 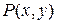(рис. 7.4), получим:

,

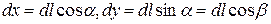где 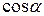и 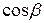– направляющие косинусы вектора .

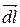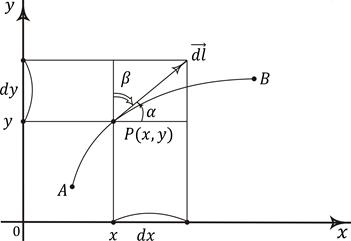
Рис. 7.4. Векторный элемент касательной к кривой в точке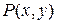

Заменяя в криволинейном интеграле второго рода 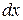и 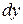найденными выражениями, получим формулу, выражающую криволинейный интеграл второго рода через криволинейный интеграл первого рода и устанавливающую связь между ними:

.

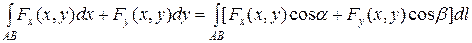Замечание. За положительное направление векторного элемента касательной принимается то, которое соответствует направлению движения точки по кривой от A к B.