2015-04-23
1466
Формула Стокса является обобщением формулы Грина и устанавливает связь между криволинейным интегралом второго рода по замкнутой кривой L и поверхностным интегралом первого рода по поверхности 
, ограниченной этой кривой.
Теорема 8.4 (без доказательства). Если функции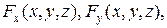 
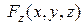непрерывны вместе со своими частными производными первого порядка на поверхности с границей L, то имеет место формула Стокса:
,
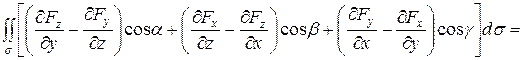
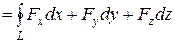где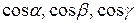 
– направляющие косинусы нормали 
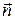к поверхности , причем направления нормали и обхода контура L подчиняются правилу правого винта (рис. 8.5).
Замечание. В частности, если поверхность – область плоскости Oxy, ограниченная контуром L, то интегралы по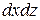 
и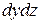 
обращаются в нуль, и формула Стокса переходит в формулу Грина.
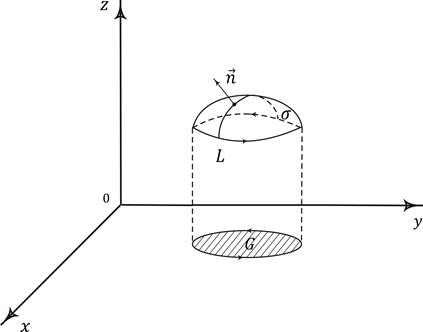
Рис. 8.5. Поверхность с границей L в формуле Стокса
