Пусть векторная функция
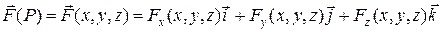
определена и непрерывна на некоторой поверхности  в пространстве
в пространстве 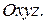
Разобьем поверхность  произвольным образом на n частей
произвольным образом на n частей  с площадями
с площадями 
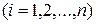 (рис. 8.3). В каждой частичной области
(рис. 8.3). В каждой частичной области 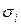 выберем произвольную точку
выберем произвольную точку 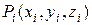 и составим сумму
и составим сумму
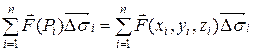 ,
,
где 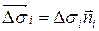 ,
, 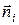 – единичная нормаль к поверхности
– единичная нормаль к поверхности  в точке
в точке 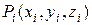 .
.
Данная сумма называется интегральной суммой для векторной функции 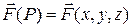 в области (на поверхности)
в области (на поверхности)  .
.
Обозначим через 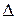 наибольший из диаметров частичных областей
наибольший из диаметров частичных областей 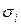 :
:
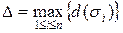 .
.
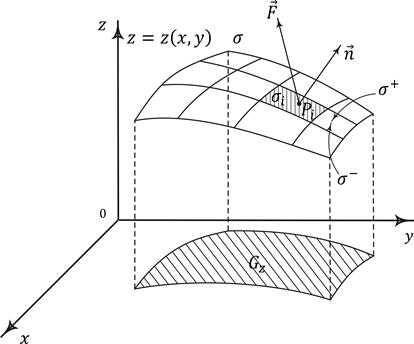
Рис. 8.3. Разбиение поверхности  на частичные области в случае
на частичные области в случае
поверхностного интеграла второго рода
Определение. Поверхностным интегралом второго рода от функции 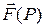 по поверхности
по поверхности  называется предел интегральных сумм при
называется предел интегральных сумм при 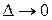 , если этот предел существует и не зависит ни от способа разбиения поверхности
, если этот предел существует и не зависит ни от способа разбиения поверхности  на частичные области
на частичные области 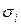 , ни от выбора в каждой из них точки
, ни от выбора в каждой из них точки 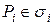 :
:
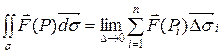
или в другой записи:
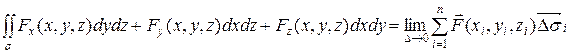 ,
,
где векторный элемент поверхности

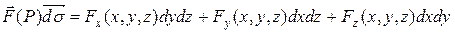 .
.
Функция
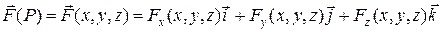
называется интегрируемой по поверхности  , сама
, сама  – поверхностью интегрирования.
– поверхностью интегрирования.
Теорема 8.2 (существования поверхностного интеграла второго рода) (без доказательства). Функция 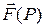 , непрерывная на кусочно-гладкой поверхности
, непрерывная на кусочно-гладкой поверхности  , интегрируема по этой поверхности.
, интегрируема по этой поверхности.
Основные свойства поверхностного интеграла второго рода аналогичны соответствующим свойствам поверхностного интеграла первого рода, за исключением свойства 5:
При изменении стороны поверхности интегрирования интеграл изменяет знак (так как переход к другой стороне поверхности меняет направление нормали к поверхности на противоположное):
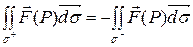 ,
,
где 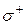 и
и 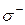 – стороны поверхности интегрирования
– стороны поверхности интегрирования  .
.
Простейший физический смысл поверхностного интеграла второго рода – количество жидкости или газа, протекающего за единицу времени в заданном направлении через поверхность  с установившейся скоростью
с установившейся скоростью 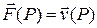 .
.
Вычисление поверхностного интеграла второго рода сводится к вычислению суммы трех двойных интегралов следующим способом.
Если 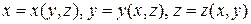 – выражения, полученные из уравнения поверхности
– выражения, полученные из уравнения поверхности  разрешением относительно соответствующих координат;
разрешением относительно соответствующих координат; 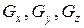 – проекции поверхности
– проекции поверхности  соответственно на плоскости
соответственно на плоскости 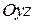 ,
, 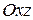 ,
, 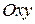 ;
; 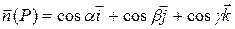 – единичная нормаль к поверхности
– единичная нормаль к поверхности  в точке
в точке 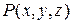 (рис. 8.3), то
(рис. 8.3), то
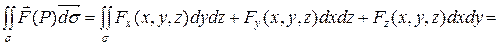
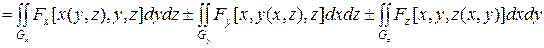 ,
,
где знаки у двойных интегралов соответствуют знакам направляющих косинусов 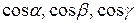 нормали
нормали 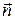 к поверхности
к поверхности  .
.
Пример. Вычислить поверхностный интеграл второго рода
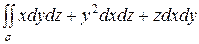 ,
,
где  – верхняя сторона плоскости
– верхняя сторона плоскости 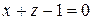 , отсеченная плоскостями
, отсеченная плоскостями 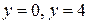 и лежащая в первом октанте (рис. 8.4).
и лежащая в первом октанте (рис. 8.4).
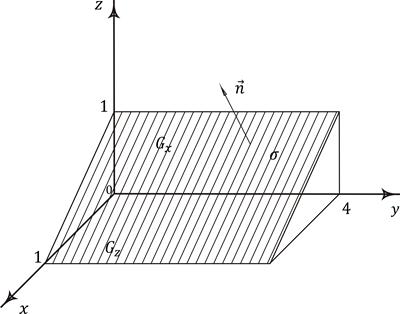
Рис. 8.4. Пример вычисления поверхностного интеграла второго рода
Обозначим через 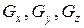 – проекции поверхности
– проекции поверхности  на плоскости
на плоскости 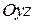 ,
, 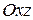 ,
, 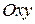 соответственно. Как видно из рис. 8.4, направляющие косинусы нормали
соответственно. Как видно из рис. 8.4, направляющие косинусы нормали 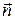 к поверхности
к поверхности 
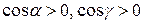 , а
, а 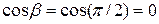 , так как плоскость
, так как плоскость  параллельна оси Oy. Следовательно, по формуле вычисления поверхностного интеграла второго рода получим:
параллельна оси Oy. Следовательно, по формуле вычисления поверхностного интеграла второго рода получим:
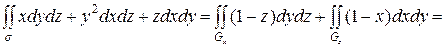
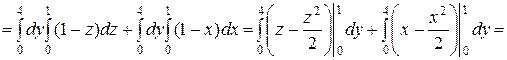
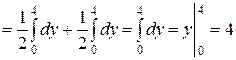 .
.
 2015-04-23
2015-04-23 13767
13767
