При решении инженерных и экономических задач часто возникает задача восстановления интерполяционного многочлена по известным значениям функции и производным в равноотстоящих узлах. Приведем два примера.
1. Пусть переменное движение материальной точки описывается по неизвестному закону 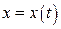 . При этом известно: координаты точек
. При этом известно: координаты точек 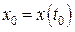 ,
, 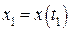 ,…,
,…, 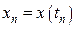 ; скоростей
; скоростей 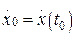 ,
, 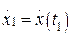 ,…,
,…, 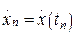 ; ускорений
; ускорений 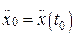 ,
, 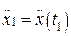 ,…,
,…, 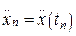 ;...и т.д. до
;...и т.д. до 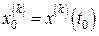 ,
, 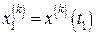 ,…,
,…, 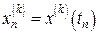 . Требуется по заданным значениям найти закон движения
. Требуется по заданным значениям найти закон движения 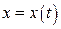 .
.
2. Пусть объем произведенной продукции описывается неизвестной функцией 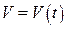 . При этом известно: количество продукции
. При этом известно: количество продукции 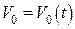 ,
, 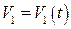 ,…,
,…, 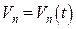 ; производительность труда
; производительность труда 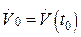 ,
, 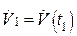 ,…,
,…, 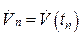 . При этом некоторые данные могут отсутствовать. Требуется по заданным значениям восстановить неизвестную функцию и значения.
. При этом некоторые данные могут отсутствовать. Требуется по заданным значениям восстановить неизвестную функцию и значения.
Итак, имеем следующую постановку задачи.
Пусть функция 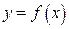 задана в равноотстоящих узлах
задана в равноотстоящих узлах 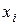 , где
, где 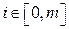 , и имеется информация о значениях производных произвольного порядка в этих точках, то есть
, и имеется информация о значениях производных произвольного порядка в этих точках, то есть
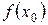 ,
, 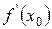 ,
, 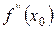 ,….,
,…., 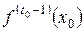 — всего
— всего 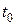 значений;
значений;
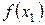 ,
, 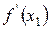 ,
, 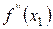 ,….,
,…., 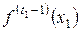 — всего
— всего 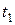 значений;
значений;
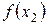 ,
, 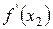 ,
, 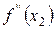 ,….,
,…., 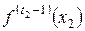 — всего
— всего 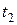 значений;
значений;
… … … … … … … … …
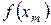 ,
, 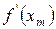 ,
, 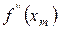 ,….,
,…., 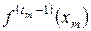 — всего
— всего 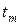 значений.
значений.
В общем случае 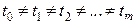 , кроме того, информация об промежуточных производных может отсутствовать.
, кроме того, информация об промежуточных производных может отсутствовать.
Необходимо получить явный вид функции 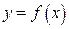 .
.
Будем называть узел 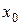 , в котором определена
, в котором определена 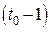 производная, узлом кратности
производная, узлом кратности 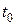 ; узел
; узел 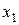 в котором определена
в котором определена 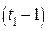 - производная, узлом кратности
- производная, узлом кратности 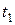 ; и т.д… узел
; и т.д… узел 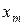 в котором определена
в котором определена 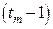 - производная, узлом кратности
- производная, узлом кратности 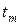 .
.
Решение задачи о нахождении явного вида функции 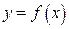 будем называть задачей о кратных узлах, а сам полином, аппроксимирующий функцию — полиномом Эрмита.
будем называть задачей о кратных узлах, а сам полином, аппроксимирующий функцию — полиномом Эрмита.
Поиск общего вида интерполяционного многочлена Эрмита представляет сложную задачу и требует привлечения математического аппарата теории функции комплексного переменного и выходит за рамки настоящего курса.
Можно показать, что искомый многочлен будет n- ой степени, которая определяется из равенства 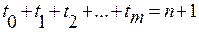 , а его аналитическая форма определяется выражением
, а его аналитическая форма определяется выражением
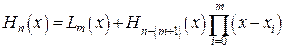 (42)
(42)
где 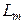 - многочлен Лагранжа m-ой степени, построенный по m известным значениям функции
- многочлен Лагранжа m-ой степени, построенный по m известным значениям функции  ,
, 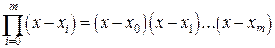 - многочлен степени m+ 1.
- многочлен степени m+ 1.
Формула (42) составлена из следующих соображений. В узлах, при 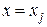 , где
, где 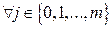 , второе слагаемое равно нулю, и значения функции в этих точках равны
, второе слагаемое равно нулю, и значения функции в этих точках равны 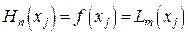 . Таким образом, выражение (42) представляет собой выделение многочлена Лагранжа из многочлена Эрмита, а второе слагаемое степени n должно обращаться в нуль в узловых точках и состоит из произведения многочлена m+ 1 степени[3] и неизвестного многочлена
. Таким образом, выражение (42) представляет собой выделение многочлена Лагранжа из многочлена Эрмита, а второе слагаемое степени n должно обращаться в нуль в узловых точках и состоит из произведения многочлена m+ 1 степени[3] и неизвестного многочлена 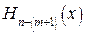 , для определения которого продифференцируем (42)
, для определения которого продифференцируем (42)
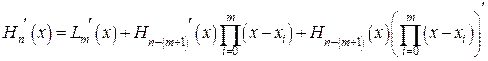 (43)
(43)
В узловых точках, второе слагаемое равно нулю, и
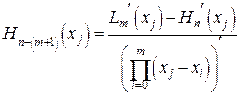 (44)
(44)
Если информация об интерполируемой функции исчерпывается данными об ее первых производных, то формула (41) будет окончательной и достаточной для восстановления неизвестной функции простым методом Лагранжа. Если известны производные более высоких порядков, то процесс дифференцирования (39) продолжают 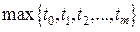 - раз, т.е. до максимальной кратности.
- раз, т.е. до максимальной кратности.
Пример 6. Пусть некоторая функция 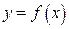 задана в виде
задана в виде
| i | x | 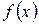 | 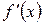 | 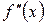 |
Требуется найти многочлен Эрмита, для которого: 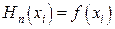 ;
; 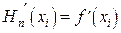 ;
; 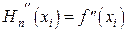 , для
, для 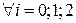 .
.
 2015-04-23
2015-04-23 4150
4150








