Интерполяция на больших отрезках, т.е. с относительно большим количеством узловых точек, имеет дополнительные трудности. С одной стороны, при больших расстояниях между узловыми точками точность очень мала, а с другой стороны, интерполяционные многочлены высокого порядка на концах отрезка значительно колеблются, что существенно искажает поведение функции. Это становится особенно важно при последующем дифференцировании.
Отчасти при решении таких задач оказывает помощь кусочная интерполяция более низкого порядка: интерполяция осуществляется по небольшому количеству узловых точек отрезка, а затем многочлены объединяют в общую интерполяционную функцию. При этом в точках стыковки обычно терпит разрыв уже первая производная.
Для получения интерполяционных формул с гладкими производными имеет смысл применить т.н. сплайн-интерполяцию функции 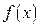 .В приложениях часто бывает достаточно применить кубическую сплайн-интерполяцию.
.В приложениях часто бывает достаточно применить кубическую сплайн-интерполяцию.
Определение. Кубическим сплайном, соответствующим непрерывной на отрезке 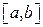 таблично заданной функции
таблично заданной функции 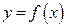 :
:
| i | ... | ... | n- 1 | n | ||
| xi | x 0 | x 1 | … | … | xn- 1 | x n |
| yi | y 0 | y 1 | … | … | yn- 1 | yn |
и узлам 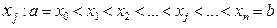 называется функция
называется функция 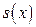 удовлетворяющая следующим условиям:
удовлетворяющая следующим условиям:
1. На каждом частичном сегменте 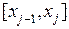 функция
функция 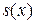 является многочленом третьей степени;
является многочленом третьей степени;
2. Значения функции 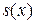 в узлах интерполяции равны значениям функции
в узлах интерполяции равны значениям функции 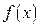 :
: 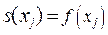 ;
;
3. Функция 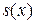 , ее первая и вторая производные непрерывны в узловых точках.
, ее первая и вторая производные непрерывны в узловых точках.
По определению кубический сплайн можно представить в виде
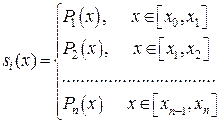
где 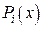 на каждом частичном сегменте есть многочлен степени не выше третьей:
на каждом частичном сегменте есть многочлен степени не выше третьей:
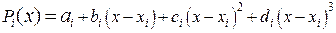 (45)
(45)
где 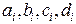 - неизвестные коэффициенты (всего 4 n – неизвестных).
- неизвестные коэффициенты (всего 4 n – неизвестных).
Используя условие (2), определяем n – неизвестных коэффициентов:
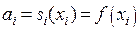 (46)
(46)
Таким образом, необходимо определить 3 n – неизвестных коэффициентов 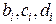 .
.
Условие непрерывности 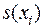 в точках
в точках 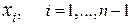 приводит к равенствам:
приводит к равенствам:
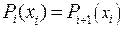
Или в соответствии с (45) и с (46)
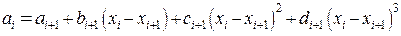 (47)
(47)
Обозначив длину интервала 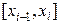 как
как
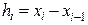 ,
,
перепишем (47) с учетом (45)
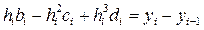 (48)
(48)
Дифференцируя (45) и накладывая условие непрерывности первой производной 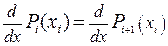 в узлах, получаем еще n - уравнений
в узлах, получаем еще n - уравнений
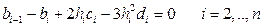 (49)
(49)
Далее непрерывность второй производной 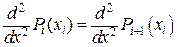 , дает нам основание записать
, дает нам основание записать
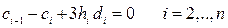 (50)
(50)
Совокупность уравнений (48)-(50) образует систему (3 n -2) – уравнений относительно 3 n - неизвестных 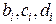 .
.
Для её однозначного решения необходимо добавить два недостающих уравнений, которые можно получить задав условия на краях интервала. В частности, можно потребовать нулевой кривизны первой производной функции на краях интервала, то есть 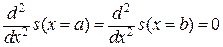 или с учетом (47)
или с учетом (47)
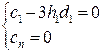 (51)
(51)
Таким образом мы получили систему 3 n - уравнений (48-51) относительно 3 n - неизвестных 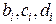 .
.
Из уравнения (48) выразим 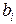 :
:
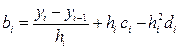 (52)
(52)
Понижая индекс суммирования на единицу
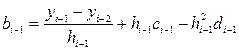 (53)
(53)
и вычитая (52) из (53), далее подставляя полученную разность 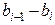 в (49), после простых преобразований получим
в (49), после простых преобразований получим
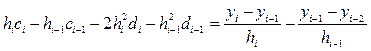 (54)
(54)
Из уравнения (50) имеем:
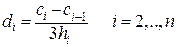 (55)
(55)
Подставляя (55) в (54), получим
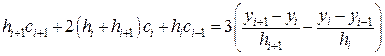 (56)
(56)
Неизвестные координаты 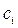 находим из последнего уравнения. Подставив их в (55) определим
находим из последнего уравнения. Подставив их в (55) определим 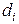 , а затем с помощью (52) и
, а затем с помощью (52) и 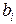 .
.
 2015-04-23
2015-04-23 628
628








