Пример 1. Найдем математическое ожидание случайной величины Х – числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных. Составим ряд распределения для Х. Из условия задачи следует, что Х может принимать значения 1, 2, 3. 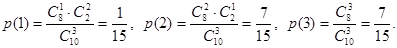 Тогда
Тогда
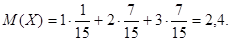
Пример 2. Определим математическое ожидание случайной величины Х – числа бросков монеты до первого появления герба. Эта величина может принимать бесконечное число значений (множество возможных значений есть множество натуральных чисел). Ряд ее распределения имеет вид:
| ξ | … | п | … | ||
| р | 0,5 | (0,5)2 | … | (0,5) п | … |
Тогда 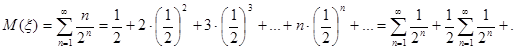 ..+
..+
+ 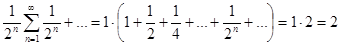 (при вычислении дважды использовалась формула суммы бесконечно убывающей геометрической прогрессии:
(при вычислении дважды использовалась формула суммы бесконечно убывающей геометрической прогрессии: 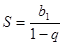 , откуда
, откуда 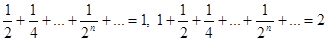 ).
).
Дисперсия.
Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида
| ξ1 | |||
| р | 0,1 | 0,8 | 0,1 |
| ξ2 | ||
| p | 0,5 | 0,5 |
Найдем М (ξ1) = 49·0,1 + 50·0,8 + 51·0,1 = 50, М (ξ2) = 0·0,5 + 100·0,5 = 50. Как видно, математические ожидания обеих величин равны, но если для ξ1 М (ξ1) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (при-чем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят от М (ξ2). Следовательно, наряду с математическим ожиданием желательно знать, на-сколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Определение.
Наряду с числовыми характеристиками положения вводят и другие числовые характеристики. Например, для того чтобы оценить рассеяние случайных величин вокруг математического ожидания, пользуются числовой характеристикой, которую называют дисперсией. Дисперсией называется математическое ожидание квадрата
отклонения случайной величины ξ от своего математического ожидания.
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
D (ξ) = M (ξ – M (ξ))².
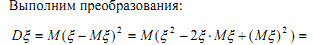
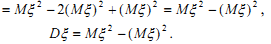
Для дискретной случайной величины ξ с законом распределения (xi, pi) дисперсия равна 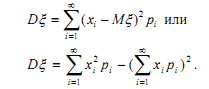

Пример.
Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных) в примере 1 данной лекции. Вычислим значения квадрата отклонения каждого возможно-го значения от математического ожидания:
(1 – 2,4)2 = 1,96; (2 – 2,4)2 = 0,16; (3 – 2,4)2 = 0,36. Следовательно,
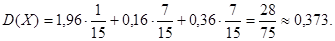
Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.
Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.
Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:
Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.

Свойства дисперсии.
1) Дисперсия постоянной величины С равна нулю:
D (C) = 0. (7.8)
Доказательство. D (C) = M ((C – M (C))²) = M ((C – C)²) = M (0) = 0.
2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
D (CX) = C ² D (X). (7.9)
Доказательство. D (CX) = M ((CX – M (CX))²) = M ((CX – CM (X))²) = M (C ²(X – M (X))²) =
= C ² D (X).
3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
D (X + Y) = D (X) + D (Y). (7.10)
Доказательство. D (X + Y) = M (X ² + 2 XY + Y ²) – (M (X) + M (Y))² = M (X ²) + 2 M (X) M (Y) +
+ M (Y ²) – M ²(X) – 2 M (X) M (Y) – M ²(Y) = (M (X ²) – M ²(X)) + (M (Y ²) – M ²(Y)) = D (X) + D (Y).
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.
Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.
4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D (X – Y) = D (X) + D (Y). (7.11)
Доказательство. D (X – Y) = D (X) + D (- Y) = D (X) + (-1)² D (Y) = D (X) + D (X).
Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.
Определение Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:
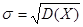 . (7.12)
. (7.12)
Пример. В предыдущем примере средние квадратические отклонения Х и Y равны соответственно 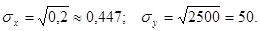
Тема 9. Определение числовых характеристик наиболее употребительных распределений непрерывных случайных величин.
Распространим определения числовых характеристик случайных величин на непре-рывные случайные величины, для которых плотность распределения служит в некото-ром роде аналогом понятия вероятности.
Определение. Математическим ожиданием непрерывной случайной величины называется
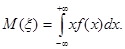 (7.13)
(7.13)
Замечание 1. Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной (опр. 7.5), а формула для ее вычисления имеет вид:
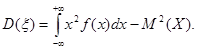 (7.14)
(7.14)
Среднее квадратическое отклонение вычисляется по формуле 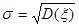 .
.
Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [ a, b ], то интегралы в формулах (7.13) и (7.14) вычисляются в этих пределах.

Пример.
Плотность распределения случайной величины ξ имеет вид:
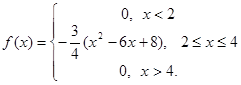
Найти М (ξ), D (ξ), σ.
Решение. 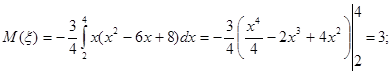
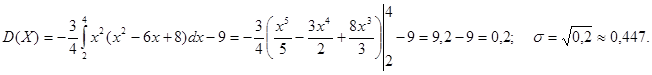
 2015-04-23
2015-04-23 7365
7365
