Числовые характеристики случайных величин

Тема 8. Определение числовых характеристик наиболее употребительных распределений дискретных случайных величин.

Числовые характеристики положения

Закон распределения (функция распределения и ряд распределения или плотность вероятности) полностью описывает случайную величину с вероятностной точки зрения, поведение случайной величины. Но часто для практических задач достаточно указать только отдельные числовые параметры, которые позволяют в сжатой форме выразить наиболее существенные черты распределения. В ряде задач достаточно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный вопрос. Такие параметры называются

числовыми характеристиками случайной величины.

Среди числовых характеристик можно выделить характеристики положения (математическое ожидание, мода, медиана), то есть некие средние, ориентировочные значения случайной величины, около которых группируются ее возможные значения.

• Рассмотрим основные числовые характеристики дискретных случайных величин.

Определение:

Математическим ожиданием дискретной случайной величины ξ называется сумма произведений всевозможных ее значений на вероятности этих значений.

Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:

М (ξ) = х ₁ р ₁ + х ₂ р ₂ + … + х_пр_п.

Если число возможных значений случайной величины бесконечно, то 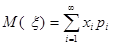, если полученный ряд сходится абсолютно.

Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.

Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.

Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непрерывных случайных величин.

Замечание 4. Если математическое ожидание равно бесконечности, то говорят, что оно не существует.