Коэффициент передачи мощности ФНЧ при чебышевской аппроксимации задается формулой:
Кр(wн) = 1/ (1 + e2 Tn2(wн), (8.10)
где e < 1 – постоянное число, называемое коэффициентом неравномерности характеристики в полосе пропускания, Тn(wн) – многочлен Чебышева n-го порядка, определяемый формулой Tn(x) = cos (n arccos x). Функция Tn(x) при любом n может быть найдена из рекуррентного соотношения:
Tn(x) = 2x Tn-1(x) - Tn-2(x), (8.11)
где Т0(х) = 1 и Т1(х) = х.
Эти многочлены часто используются в задачах аппроксимации благодаря следующему свойству: среди всех многочленов n-ой степени с одинаковыми коэффициентами при старшей степени аргумента эти многочлены менее всего уклоняются от нуля на интервале -1 < x < 1. В то же время при /x/ >> 1 многочлены Чебышева резко увеличивают свои значения. Асимптотически Tn(x)» 2n-1 xn, /x/ >> 1.
С помощью таких функций можно удачно аппроксимировать идеальную характеристику ФНЧ: из (8.10) видно, что в пределах полосы пропускания фильтра величина К(р) колеблется от 1 до 1/(1 + e2); при wн >> 1 фильтр обеспечивает большое ослабление сигнала.
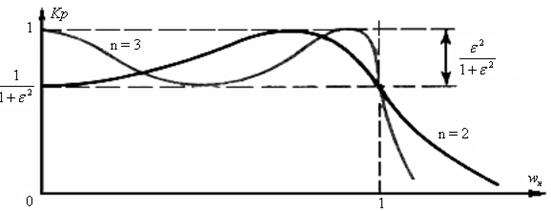
Рис. 8.10 – ЧКПМ фильтра Чебышева.
Из графиков частотных характеристик передачи мощности для двух чебышевских фильтров при n = 2 и n = 3 видно, что в полосе пропускания эти функции немонотонны. Величина пульсаций ослабления тем выше, чем больше e. Из (8.10) следует, что увеличение e ведет к большему ослаблению сигналов вне полосы пропускания. Подбором двух параметров n и e можно добиться выполнения исходных условий, предъявляемых к синтезируемому фильтру.
Передаточная функция чебышевского ФНЧ. Из (8.10) видно, что полюсы коэффициента передачи мощности чебышевского фильтра являются корнями уравнения
1 + e2 Tn2(рн) = 0. (8.12)
Метод решения данного уравнения довольно громоздок, поэтому ограничимся его результатами. Сначала необходимо вычислить вспомогательный параметр:
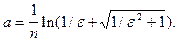 (8.13)
(8.13)
Затем должны быть найдены полюса фильтра Баттерворта того же порядка. Переход к полюсам чебышевского фильтра осуществляется за счет того, что абсцисса каждого полюса фильтра Баттерворта умножается на sh a, а ордината - на ch a. Если полюса фильтра Баттерворта располагаются на единичной окружности, то полюса чебышевского фильтра лежат на эллипсе, уравнение которого в плоскости рн = sн + jwн имеет вид:
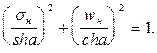
Получив координаты полюсов, можно записать выражение передаточной функции чебышевского фильтра в виде:
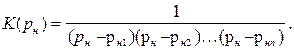 (8.14)
(8.14)
 2015-04-23
2015-04-23 1207
1207
