Системы параметров 4-полюсников

Линейные 4-полюсники (и пассивные, и активные) могут быть приведены к единой схеме замещения. Для определения параметров схемы замещения используют соотношения между комплексными амплитудами напряжений и токов.

Схема замещения 4-полюсника может быть представлена в системах Y-, Z-, A- и H-параметров.

Если исходными являются комплексные амплитуды входного и выходного напряжений, то уравнения для искомых токов запишутся следующим образом:

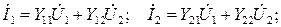
или в матричной форме: 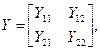при этом Y-параметры имеют размерность и физический смысл проводимости: 11 – входная; 12 – передаточная в обратном направлении (обратной передачи); 21 – передаточная; 22 – выходная.

Для определения комплексных амплитуд напряжений относительно заданных входного и выходного токов используются следующие уравнения:

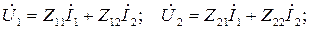
или в матричной форме: 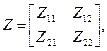при этом Z-параметры имеют размерность и физический смысл сопротивления: 11 – входное; 12 – передаточное в обратном направлении (обратной передачи); 21 – передаточное; 22 – выходное (холостого хода).

Система Н-параметров определяется из следующих уравнений (исходными являются входной ток и выходное напряжение):

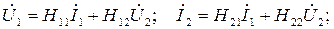
или в матричной форме: 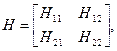при этом Н-параметры имеют различные размерности и физический смысл: 11 – входное сопротивление; 22 – выходная проводимость; 12 – коэффициент обратной передачи напряжения и 21 – коэффициент передачи (для активных – усиления) по току – безразмерные величины.

И, наконец, система А-параметров (или обобщенных параметров) задается относительно известных выходных комплексных амплитуд напряжения и тока:

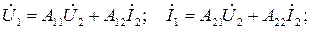
при этом А-параметры имеют следующий физический смысл и размерность: 11 – коэффициент обратной передачи напряжения (аналог Н₁₂); 12 – сопротивление обратной передачи (аналог Z₁₂); 21 – проводимость обратной передачи (аналог Y₁₂); 22 – коэффициент обратной передачи (усиления) по току.

Параметры схем замещения могут быть определены в режиме короткого замыкания или холостого хода со стороны входа или выхода 4-полюсника, т.е. при равенстве нулю одной из заданных комплексных амплитуд:

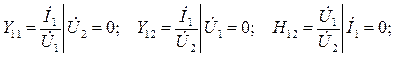и т.д.

Активные 4-полюсники в отличие от пассивных, как правило необратимы, т.е. принцип (теорема) взаимности к ним неприменим: Y₁₂ ≠ Y₂₁; Z₁₂ ≠ Z₂₁; H₁₂ ≠ H₂₁.

Все формы уравнений передачи принципиально равноправны. Выбор той или иной формы зависит исключительно от решаемой задачи.

Два четырехполюсника, имеющие одинаковые системы параметров, независимо от их внутренней структуры, числа элементов и т. д., характеризуются одинаковыми уравнениями передачи. Такие четырехполюсники называются эквивалентными, и при включении любого из них между одними и теми же внешними цепями на их зажимах устанавливаются одинаковые режимы.

Системы Y-, Z-, A- и H-параметров образованы из коэффициентов уравнений передачи, и поэтому часто их объединяют одним названием параметры-коэффициенты. Рассмотрим основные свойства параметров-коэффициентов.

1. Параметры-коэффициенты определяются только схемой четырехполюсника и её элементами и не зависят от внешних цепей, между которыми он включен, т. е. они характеризуют собственно четырехполюсник.

2. Все системы параметров-коэффициентов описывают один и тот же четырехполюсник, поэтому между ними существует однозначная взаимосвязь.

3. Пассивный четырехполюсник полностью характеризуется не более чем тремя независимыми параметрами.

4. Симметричные пассивные четырехполюсники имеют только два независимых параметра, для них выполняется принцип взаимности.

5. Параметры-коэффициенты имеют определённый физический смысл. Для выявления этого физического смысла следует четырехполюсник поставить в такой режим работы, при котором уравнения передачи будут содержать лишь один интересующий параметр. Такое произойдет если использовать режим холостого хода или режим короткого замыкания.

6. Из предыдущего свойства следует, что параметры-коэффициенты являются комплексными величинами, так как они определяются отношением комплексных амплитуд напряжений и токов. При рассмотрении их в частотной (спектральной) области они будут рациональными функциями оператора (iw); при переходе к комплексной частоте р – ее функциями.

7. 5 Передаточная функция четырехполюсника и ее свойства

В дальнейшем в качестве аргумента частотного коэффициента передачи будет использоваться не только переменная iw, но и комплексная частота р, т.е. наряду с функцией K(iw) рассматривается более общая характеристика – передаточная функция К(р). Передаточная функция линейного 4-полюсника является его основной частотной характеристикой и определяется в стационарном режиме как отношение комплексной амплитуды сигнала на выходе к комплексной амплитуде сигнала на входе при гармоническом воздействии. В зависимости от характера входных и выходных сигналов передаточная функция может иметь размерность проводимости: K_Y = I₂ / U₁;

сопротивления: K_Z = U₂ / I₁; либо быть безразмерной величиной: K(p) = U₂ / U₁;

K(p) = I₂ / I₁ (комплексный коэффициент передачи по напряжению или току). При этом для активных 4-полюсников они будут называться соответственно коэффициентами усиления. Необходимо отметить, что значение передаточной функции K(р) зависит от направления передачи энергии в системе. Если источник и нагрузка меняются местами, то следует ввести коэффициент передачи в обратном направлении:

К_обр(р) = U₁/U₂.

Коэффициенты прямой и обратной передачи в общем случае не совпадают.

Передаточная функция четырехполюсника обладает всеми свойствами аналогичных функций линейных стационарных систем. Так, линейному четырехполюснику с постоянными параметрами отвечает функция

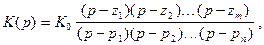(7.12)

где К₀ - постоянная величина. Рассмотрим свойства передаточной функции (условия устойчивости и физической реализуемости 4-полюсников):

1. Она является дробно-рациональной функцией с вещественными коэффициентами, что обусловлено постоянными параметрами элементов схемы 4-полюсника.

2. Чтобы синтезируемая цепь была устойчива, полюсы р₁, р₂,..., р_n должны располагаться в левой полуплоскости, образуя комплексно-сопряженные пары.

3. Число полюсов функции К(р) должно превышать число нулей, т.е. в бесконечно удаленной точке должен существовать не нуль, а полюс передаточной функции. В противном случае в пределе (при стремлении частоты к бесконечности) АЧХ принимала бы бесконечно большое значение, т.е. 4-полюсник обладал бы бесконечно большим усилением.

4. В отличие от входного сопротивления двухполюсника разность числа нулей и полюсов передаточной функции может быть сколь угодно большой. Это связано с тем, что на фазовый угол коэффициента передачи не могут быть наложены какие-либо энергетические ограничения.

5. Расположение нулей передаточной функции. В отличие от полюсов нули функции К(р) устойчивого линейного четырехполюсника могут располагаться как в левой, так и в правой полуплоскости переменной р. Действительно, характеристическое уравнение К(р) = 0 означает, что при некотором входном U₁(p) ¹ 0 изображение выходного напряжения U₂(p) обращается в нуль. Это не противоречит предположению об устойчивости системы.

Четырехполюсники, не имеющие нулей передаточной функции в правой полуплоскости, называют минимально-фазовыми цепями. Если же нули в правой полуплоскости имеются, то такие четырехполюсники называют неминимально-фазовыми цепями. При одинаковом числе нулей и полюсов неминимально-фазовая цепь обеспечивает большее по абсолютной величине изменение фазы коэффициента передачи по сравнению с минимально-фазовой цепью.

Расположение нулей функции К(р) связано с топологической структурой цепи. В теории цепей показывается, что минимально-фазовым будет любой четырехполюсник со следующим свойством: передача сигнала со входа на выход может быть полностью прекращена путем разрыва единственной ветви. В частности, минимально-фазовыми оказываются любые четырехполюсники лестничной структуры.

Неминимально-фазовые цепи имеют, как правило, структуру мостовых (скрещенных) схем, в которых сигнал на выход проходит по двум каналам или более. Простейший пример неминимально-фазовой цепи – симметричный мостовой четырехполюсник, образованный элементами R и С. Здесь, как легко убедиться,

K(p) = (pRC - 1)/(pRC + 1).

Данная функция имеет нуль передаточной функции в точке p = 1/(RC), т.е. в правой полуплоскости.

Однако мостовая структура не гарантирует автоматически принадлежность цепи к минимально-фазовому классу и в каждом отдельном случае следует проверять наличие или отсутствие нулей в правой полуплоскости.

Связь между модулем и фазой частотного коэффициента передачи. Доказано, что четырехполюсники минимально-фазового типа обладают замечательной особенностью: модуль и фаза их частотного коэффициента передачи, т.е. АЧХ и ФЧХ этих цепей, однозначно связаны друг с другом. Вещественная и мнимая части логарифма частотного коэффициента передачи

ln {/K(jw)/ exp[jj_K(w)]} = ln /K(jw)/ + jj_K(w) = y_K(w) + jj_K(w)

образуют пару преобразований Гильберта:

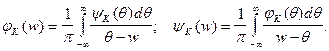(7.13)

В четырехполюснике минимально-фазового типа невозможно, реализуя заданную АЧХ, получить любую ФЧХ. Так, если АЧХ минимально-фазового четырехполюсника на какой-нибудь частоте достигает максимума, то ФЧХ в окрестности этой частоты проходит через нуль. Если же четырехполюсник принадлежит к классу цепей неминимальной фазы, то АЧХ и ФЧХ независимы друг от друга. Среди неминимально-фазовых цепей особо важную роль играют так называемые всепропускающие четырехполюсники, у которых модуль коэффициента передачи постоянен и не зависит от частоты. Примером может служить симметричный мостовой RC-четырехполюсник, для которого

/K(iw)/ = 1; j_K = -2 arctg wRC.

Подобные четырехполюсники используются для целей фазовой коррекции сигналов. Они позволяют частично компенсировать искажения формы сигналов, прошедших через радиотехнические устройства.

Коэффициент передачи мощности. Как известно, коэффициент передачи мощности – это квадрат модуля частотного коэффициента передачи четырехполюсника:

K_p(w) = K(iw) K*(iw) = K(iw) K(-iw). (7.14)

В отличие от самого коэффициента передачи K(iw) функция K_p(w) вещественна и положительна (по определению квадрата модуля) и поэтому особенно удобна для задания исходных данных к синтезу четырехполюсника. Однако она не содержит сведений о ФЧХ системы. Как видно из (7.14), коэффициент передачи мощности – четная функция частоты с вещественными коэффициентами, и поэтому он всегда может быть представлен в виде отношения двух многочленов по степеням w²:

K_p(w) = M(w²) / N(w²). (7.15)

И в предельном случае при стремлении частоты к бесконечности не будет принимать бесконечного значения, т.к. m ≤ n.

При замене переменной p = iw функция К_р(w) аналитически продолжается с мнимой оси jw на всю плоскость комплексных частот:

К_р(р) = К(р) К(-р). (7.16)

Формула (7.16) устанавливает принципиальный факт: если a + jb – особая точка (нуль или полюс) функции К(р), то К_р(р) будет иметь такую же особую точку как при p = a + jb, так и при p = - a - jb. Принято говорить, что особые точки частотного коэффициента передачи мощности имеют квадрантную симметрию, т.е. располагаются на комплексной плоскости, имея центр симметрии в начале координат. Это свойство имеет большое значение для задач синтеза четырехполюсников, поскольку оно дает возможность восстанавливать частотный коэффициент передачи по известной функции К_р(р).

8. СИНТЕЗ ФИЛЬТРОВ

8.1. Общие сведения о фильтрах и их классификация.

8.2. Этапы проектирования фильтров.

8.3. ФНЧ. Фильтр Баттерворта.

8.4. Фильтр Чебышева.

8.5. Структурный синтез фильтров.

8.6. Реализация ФВЧ и ПФ.