2015-04-23
423
В любой системе частиц имеется одна замечательная точка, называемая центром масс, которая обладает рядом интересных и важных свойств. Ее положение относительно начала данной системы координат характеризуется радиус-вектором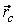 
, определяемым как
 ,
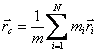| (2.10) |
где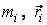 
– масса и радиус-вектор 
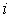-й частицы, 
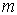– масса всей системы, 
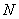– полное число частиц в системе. Если взять производную по времени от обеих частей уравнения и умножить обе части на 
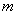, то получится:
или
,
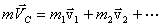где 
– скорость движения центра масс системы. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость ее центра масс:
.
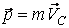Подставив это выражение в (2.9), получим:
 .
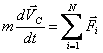| (2.11) |
Отсюда следует, что центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы. Этот результат называется теоремой о движении центра масс системы материальных точек. Уравнение (2.11) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на систему материальных точек: ускорение системы как целого прямо пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы.
Если система замкнута, то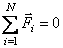 
и уравнение (2.11) переходит в 
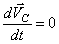, следовательно, 
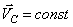. Таким образом, центр масс замкнутой системы движется прямолинейно и равномерно или покоится.
