Объединение (сумма) множеств А и В (обозначение АÈВ) есть множество всех элементов, принадлежащих множеству А или множеству В. При этом повторяющиеся элементы включаются в объединение только один раз. Объединение большего числа множеств определяется аналогично.
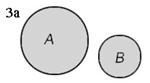
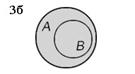
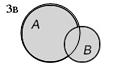
Различные случаи объединения множеств рассмотрены на рисунке 3, результаты операции объединения закрашены.
|
| 
| ||||||
| АÈВ | если ВÌА, то АÈВ=А | АÈВ | ||||||
| Рис. 3. Объединение множеств |
Примеры:
1. Пусть А — множество юношей в студенческой группе, В — множество девушек в этой же группе, тогда АÈ В=С — это множество всех студентов группы (рис. 3а).
2. Пусть А={3, 4, 5, 6} и В={ 3, 4}, тогда АÈВ={ 3, 4, 5, 6} (рис. 3б).
3. Пусть множества А и В заданы промежутками на числовой прямой А=[–1; 5] и В = [0; 1], тогда АÈ В = [–1; 5] (рис. 3в).
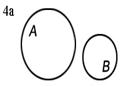
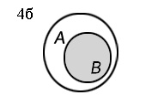
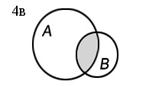
Пересечение (произведение) множеств А и В (обозначается АÇВ) есть множество, состоящее из элементов, общих для обоих множеств. Пересечение большего числа множеств определяется аналогично. На рисунке 4 изображены различные случаи пересечения множеств А и В (результат операции пересечения закрашен).
|
| 
| ||||||
| АÇВ=Æ | если ВÌА, то АÇВ=В | АÇВ | ||||||
| Рис. 4. Пересечение множеств |
Примеры:
1. Пусть А множество целых отрицательных чисел, а В — множество натуральных чисел, тогда АÇ В=Æ (рис. 4а).
2. Пусть А — множество всех целых чисел, В — множество целых отрицательных чисел, тогда АÇ В=В (рис. 4б).
3. Пусть А={3, 4, 5, 6, 7, 8, 9}, В={6, 7, 8, 9, 10, 11, 12, 13}, тогда АÇВ={6, 7, 8, 9} (рис. 4в).
4. Пусть множества А и В заданы промежутками на числовой прямой А=(–5; 2] и В = [0; 2], тогда АÇВ = [0; 2] (рис. 4б).
5. Пусть множества А и В заданы промежутками на числовой прямой А=(–5; 2] и В = [3; 7], тогда АÇВ =Æ (рис. 4а).
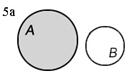
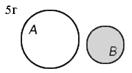
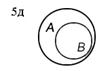
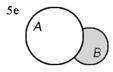
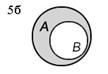
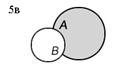
Разность множеств А и В (обозначается А\В) есть множество, состоящее из всех элементов множества А, не входящих в множество В. На рисунке 5 изображены различные случаи вычитания множеств (результат операции вычитания закрашен).
| 
| 
| |||||||||
| А\В=А | А\В | А\В | |||||||||
|
|
| |||||||||
| В\А=В | Если ВÌА, то В\А=Æ | В\А | |||||||||
| Рис. 5. Вычитание множеств |
Примеры:
1. Пусть А — множество всех целых чисел, а В — множество всех целых положительных чисел, тогда А\В — это множество всех целых отрицательных чисел (рис. 5в).
2. Пусть А={1, 2, 3, 4, 5}, В={1, 2, 3}; А\ В={4, 5} (рис. 5в).
3. По данным промежуткам А=(–3; 2] и В = [–2; 1] на числовой прямой определим АÈВ = (–3; 2] (рис. 3б); АÇВ = [–2; 1] (рис. 4б); А\В=(–3; –2)È(1; 2] (рис. 5б); В\А=Æ (рис. 5д).
 2015-04-23
2015-04-23 1659
1659