2015-04-23
936
Признак Лейбница используется при исследовании на сходимость знакочередующегося ряда.(См. п 3.4.3).
Теорема. Пусть дан знакочередующийся числовой ряд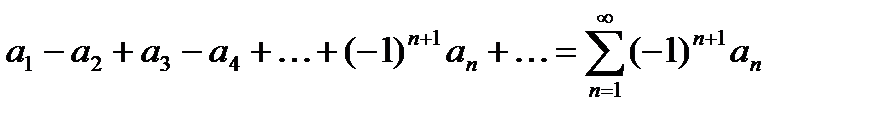 
. Знакочередующийся ряд сходится, если:
1. Последовательность абсолютных величин членов ряда монотонно убывает, т.е.
2. Общий член ряда стремится к нулю: 
Пример
Исследовать на сходимость ряд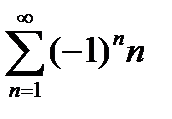 
Решение.
В общий член ряда входит множитель (-1) n, а значит, ряд является знакочередующимся и нужно использовать признак Лейбница.
Члены ряда не убывают по модулю. Да и предел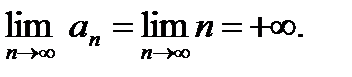 
Вывод: ряд расходится.
Знакочередующийся ряд является частным случаем знакопеременного ряда, который содержит бесконечное множество положительных и бесконечное множество отрицательных членов.
Определение. Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Определение. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
|
|
|
Пример
Исследовать на сходимость ряд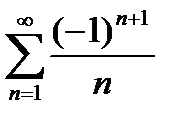 
Решение
Ряд является знакочередующимся.
Используем признак Лейбница:
1) Каждый следующий член ряда по модулю меньше, чем предыдущий: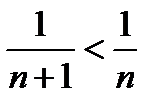 
2) Предел общего члена ряда равен нулю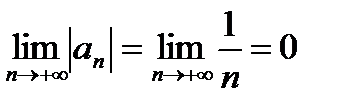 
Вывод: ряд сходится.
Выясним, как сходится данный ряд, условно или абсолютно.
Составим ряд из модулей – просто убираем множитель, который обеспечивает знакочередование:
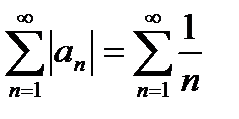– расходится (гармонический ряд).
Таким образом, исходный ряд сходится. условно.
Пример
Исследовать на сходимость ряд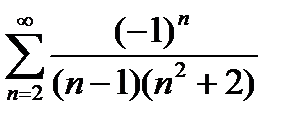 
.
Решение
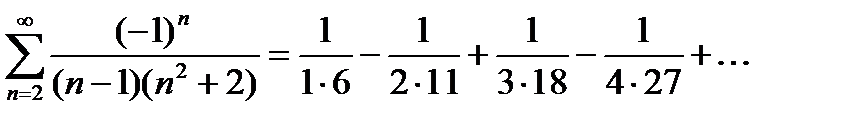
Данный ряд является знакочередующимся.
Используем признак Лейбница:
1) Каждый следующий член ряда по модулю меньше, чем предыдущий:
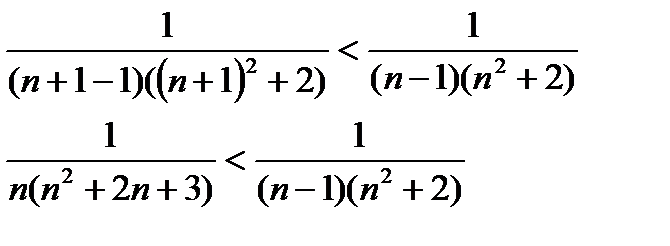
2) 
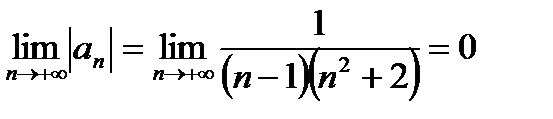
Вывод: ряд сходится.
Исследуем ряд на абсолютную сходимость:
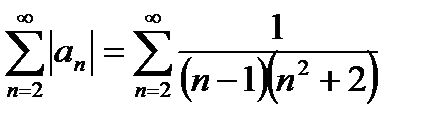
Анализируя общий член ряда, приходим к выводу, что здесь нужно использовать предельный признак сравнения. Скобки в знаменателе удобнее раскрыть:
Сравним данный ряд со сходящимся рядом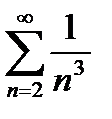 
. Используем предельный признак сравнения:
Получено конечное число, отличное от нуля, значит, ряд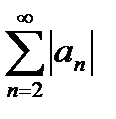 
сходится вместе с рядом .
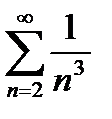Исследуемый ряд сходится абсолютно.
Продолжение следует.
