Интегральный признак Коши

Основной предпосылкой использования интегрального признака Коши является тот факт, что в общем члене ряда есть некоторая функция и её производная.

Теорема. Если члены знакоположительного ряда 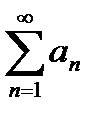могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке [1;+¥) функции f(x) так, что a₁=f(1), a₂=f(2), … a_n=f(n), то:

а) если , то ряд расходится;

б) если 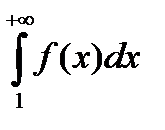равен любому конечному числу, то ряд сходится.

Замечания.

1. Функцию f(x) можно получить из общего члена ряда a_n путем замены n на x.

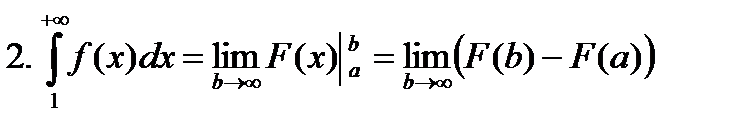- несобственный интеграл.

Пример

Исследовать на сходимость ряд .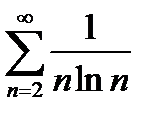

Решение

Подынтегральная функция непрерывна на [2;+¥). Используем интегральный признак:

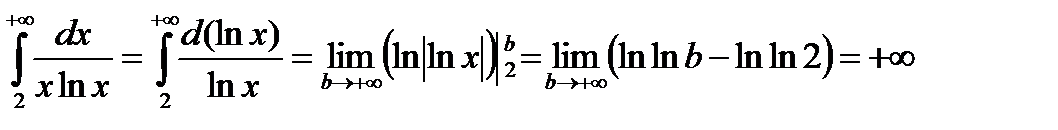
Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.

Пример

Исследовать на сходимость ряд .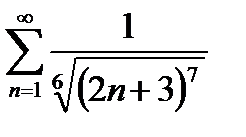

Решение

Подынтегральная функция непрерывна на [1;+¥). Используем интегральный признак Коши:

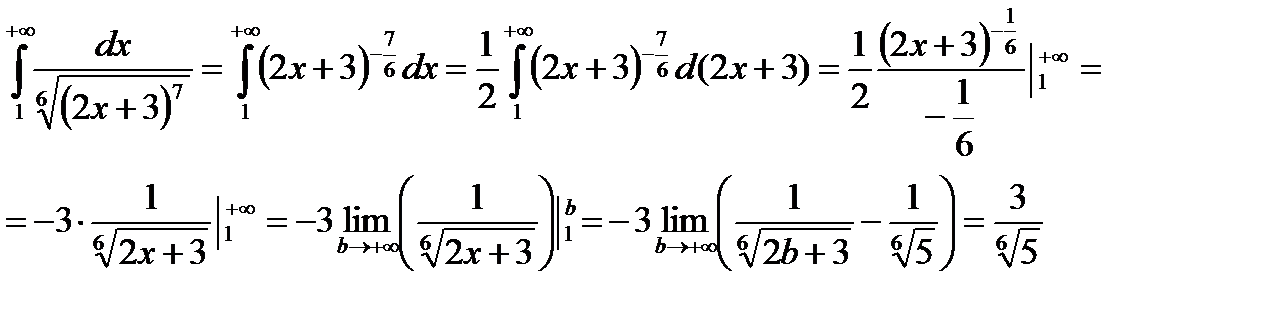
Получено конечное число, значит, исследуемый ряд сходится вместе с соответствующим несобственным интегралом.