Замечания

1. В частности, ряд сходится при .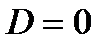

2. В частности, ряд расходится при .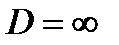

3. При 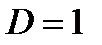признак не дает ответа. Ряд может быть как сходящимся, так и расходящимся. Нужно использовать другой признак.

Пример

Исследовать на сходимость ряд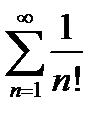

Решение

Находим D: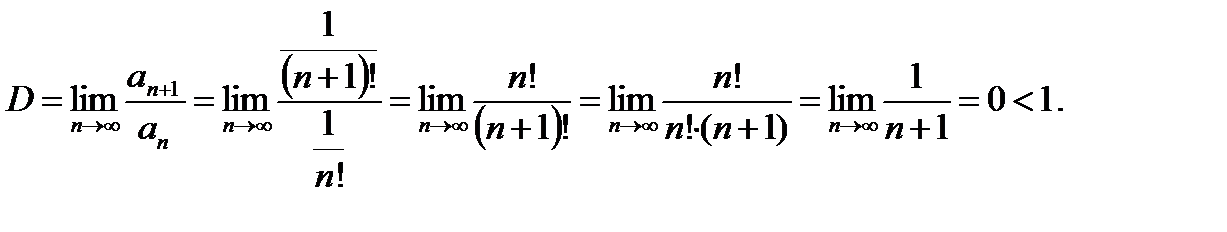

Так как D<1, то данный ряд по признаку Даламбера сходится.

Пример

Исследовать на сходимость ряд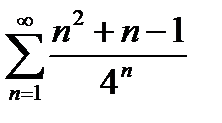

Решение

В знаменателе общего члена ряда у нас есть степень, а это верная предпосылка того, что нужно использовать признак Даламбера.

Используем признак Даламбера:

Для того, чтобы получить следующий член ряда необходимо вместо n подставить n+1: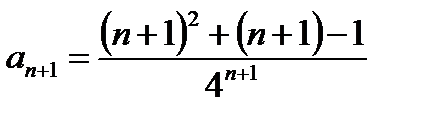

Составим отношение следующего члена ряда к предыдущему:

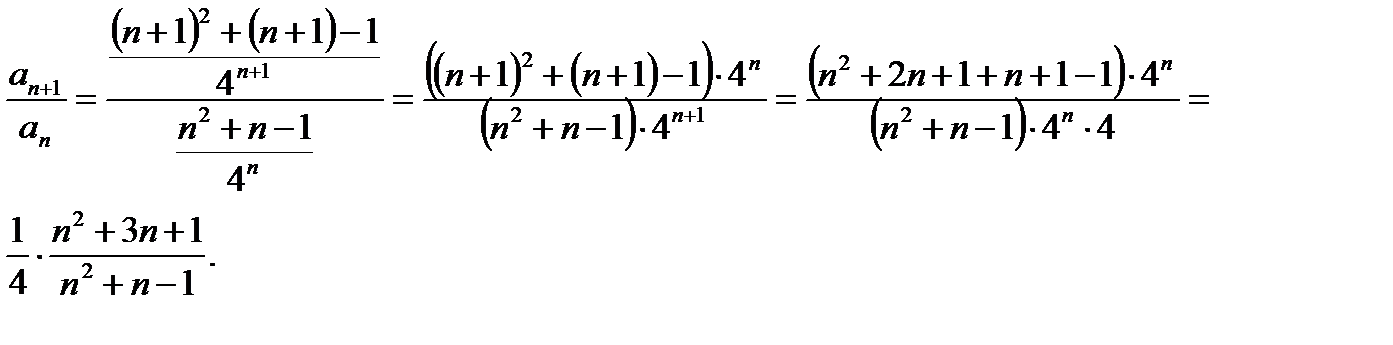
Найдем предел полученного отношения:

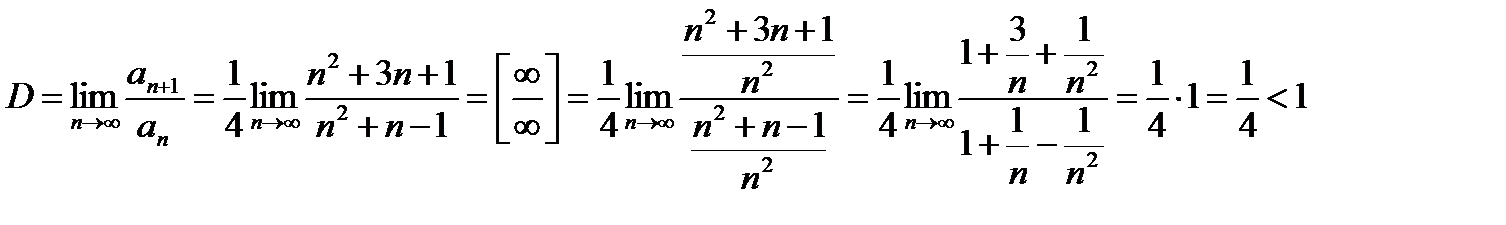
Таким образом, исследуемый ряд сходится.