Устойчивость цепей с обратной связью

Рассмотрим систему с обратной связью, образованную активным элементом с передаточной функцией К(р) и звеном обратной связи с передаточной функцией ß(р), и предположим, что эта система автономна, т.е. внешний входной сигнал не подается, т.е. U_вх(р)=0.

Уравнение состояния записывается на основании того, что

U_вых (p) = K(p)ß(p)U_вых(p),

откуда

(1 - K(p)ß(p)) U_вых(p) = 0. (4)

Поскольку изображение выходного сигнала тождественно не может быть равно нулю (в противном случае система не была бы возбуждена), то равенство (4) будет справедливо лишь при тех значениях р, которые являются корнями характеристического уравнения

1 - K(p)ß(p)= 0. (4*)

Для того, чтобы цепь с ОС была абсолютная устойчива, необходимо, чтобы корни этого уравнения имели отрицательные вещественные части, т.е. располагались в левой полуплоскости комплексной частоты.

Если синтезируемая цепь должна быть устойчивой, то необходимо определить критерии, которые по виду передаточных функций K(p) и ß(p) позволили бы судить об отсутствии корней уравнения (4) в правой полуплоскости. И наоборот, для создания неустойчивой автоколебательной системы следует знать корни (4), определяющие частоту самовозбуждения. Для нас важен первый случай, поэтому рассмотрим критерии устойчивости цепей с ОС.

Алгебраические критерии устойчивости.

Предположим, что и основной элемент, и элемент ОС являются цепями с сосредоточенными параметрами и их можно записать как отношение двух полиномов по степени частоты р:

K(p) = P₁(p)/Q₁(p); ß(p) = P₂(p)/Q₂(p) (5)

Подставляя (5) в (4*), получим:

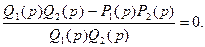(6)

Отсюда следует, что система с ОС будет устойчива, если все корни уравнения

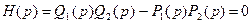(6*)

имеют отрицательные вещественные части. Полиномы Н(р) с такими свойствами называют полиномами Гурвица.

В качестве частного случая полинома Гурвица можно рассматривать передаточную функцию фильтров Баттерворта или Чебышева, имеющие один вещественный и пары комплексно-сопряженных корней, удовлетворяющих такому же условию.

Полное решение данной задачи (необходимое и достаточное условие) называется критерием Рауса-Гурвица и формулируется следующим образом:

Для того, чтобы уравнение

a_npⁿ + a_n-1p^n-1 + … + a₁p¹ + a₀ = 0

с вещественными коэффициентами имело корни лишь в левой полуплоскости переменной р, необходимо и достаточно, чтобы положительными были следующие величины:

- коэффициенты a_n, a₀;

- определитель Рауса-Гурвица и все его главные миноры (считаются по первой строке с вычеркиванием соответствующих строк и столбцов):

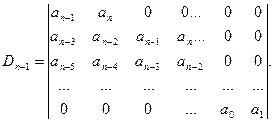
Достоинство критерия Рауса-Гурвица – относительная простота вычислений, Недостаток заключается в применимости его только для цепей с сосредоточенными параметрами, потому что только для них передаточная функция выражается через полиномы.

Геометрические (частотные) критерии устойчивости.

Возвращаясь к характеристическому уравнению 1 - K(p)ß(p) = 0, нетрудно догадаться, что произведение w (p) = K(p)ß(p) есть не что иное, как передаточная функция каскадного соединения двух звеньев – основного и звена ОС. Она называется передаточной функцией системы с разомкнутой ОС и ее можно рассматривать как отображение комплексной плоскости р на другую комплексную плоскость w. При этом корням р₁, р₂, …,р_n характеристического уравнения 1 - K(p)ß(p)= 0 в плоскости w будет соответствовать единственная точка w = 1.

Отсюда непосредственно вытекает принцип, позволяющий судить о возможности самовозбуждения системы с ОС: если образ правой полуплоскости переменной р при отображении на плоскость w содержит точку w =!, то система с замкнутой ОС неустойчива.