Критерий оптимальности линейного частотного фильтра

Используя все полученные ранее соотношения, определим отношение сигнал/шум на выходе линейного стационарного частотного фильтра. Его частотный коэффициент передачи определяется по формуле:

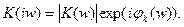
Спектральная плотность полезного входного сигнала: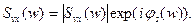

Используя спектральный метод анализа, можно определить значение выходного сигнала в любой момент времени t₀:

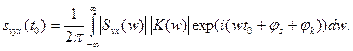(16)

Белый шум на входе при любой частоте имеет постоянный энергетический спектр (или дисперсию):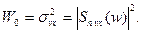

Вообще, для любого сигнала энергетический спектр (или же квадрат АЧХ – модуля спектральной плотности) связан с его автокорреляционной функцией парой преобразований Фурье. Данная функция количественно определяет степень отличия сигнала s(t) и его сдвинутой на τ копии s(t – τ) и равна их скалярному произведению:

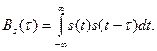
Тогда дисперсия (или энергетический спектр) шума на выходе фильтра определится как: 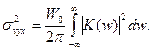(17)

Искомое отношение сигнал/шум на выходе фильтра, определяемое как модуль мгновенного значения полезного сигнала к среднеквадратичному уровню шума (14) 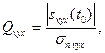при использовании неравенства Шварца (Коши-Буняковского)

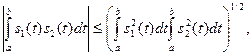(18)

для (16) и (17) можно записать следующим образом:

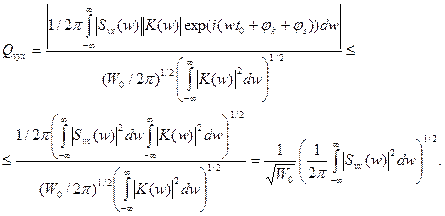
Полученное в скобках выражение есть ни что иное, как полная энергия полезного входного сигнала (равенство Парсеваля), поэтому отношение сигнал/шум на выходе фильтра можно записать в виде: 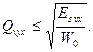(19)

Неравенство (19) определяет критерий оптимальности линейного частотного фильтра, суть которого заключается в том, что отношение сигнал/шум на выходе фильтра зависит только от отношения энергий полезного сигнала и шума на его входе.

Данное соотношение содержит полное решение поставленной задачи и позволяет, зная энергетические спектры сигнала и шума, так подобрать АЧХ фильтра, чтобы получить ощутимый выигрыш.